Calcular seno(22,5)°
To aqui me matando pra tenta fazer isso x_x . Sei q n eh complicado, mas n consigo pensar numa maneira de desmembrar. Ja tentei seno(45-22,5). Tb seno(45/2) (esse eu so montei, mas n sei a regra pra divisao, que nem tem na apostila)
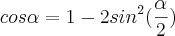
![sin(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{2}}](/latexrender/pictures/6c98d275d5d8f2fc0047e833ced5d3ca.png "sin(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{2}}")
![sin(\frac{45}{2})º=\sqrt[]{\frac{1-cos45º}{2}}=...](/latexrender/pictures/64688d8fb6822d41b2581c14af5c3752.png "sin(\frac{45}{2})º=\sqrt[]{\frac{1-cos45º}{2}}=...")
![cos(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1+cos\alpha}{2}}](/latexrender/pictures/fd14e92b142aaf3e6b8366eec580d3af.png "cos(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1+cos\alpha}{2}}")
![tg(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{1+cos\alpha}}](/latexrender/pictures/907e830076c22870ce9e3ef528694520.png "tg(\frac{\alpha}{2})=\pm\sqrt[]{\frac{1-cos\alpha}{1+cos\alpha}}")
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)