soluçao:
uma equaçao polinomial é dita reciproca quando os coeficiente obedecem a certa simetria,tais que:
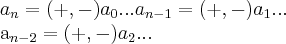
ou seja
![{a}_{k}=(+,-){a}_{n-(k-1)}...k\in[1,2,...,n] {a}_{k}=(+,-){a}_{n-(k-1)}...k\in[1,2,...,n]](/latexrender/pictures/a0beb8da7f7887762228fcfccee13aad.png)
ou de certa forma essa simetris se traduz nos "coeficientes equidistantes" da equaçao polinomial.
em nosso exercicio,temos que,pela restriçao(condiçao)colocada:
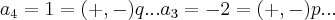
aqui temos dois polinomios,os de 1° especie,no caso
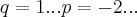
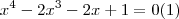
em que os "coeficientes equidistantes" sao iguais...
e
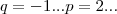
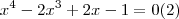
esse de segunda especie,onde os "coeficientes equidistantes sao simetricos".
"teorema:toda equaçao polinomial de segunda especie e grau par,admite 1 e -1 como raizes,logo:

é tal que:
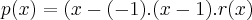

onde r(x) tera grau 2,e mais facil soluçao...resolva-o...
a equaçao de 1° especie par,tem as soluçoes de busca de raizes racionais,como fizemos anteriormente...
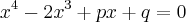

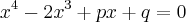

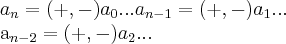
![{a}_{k}=(+,-){a}_{n-(k-1)}...k\in[1,2,...,n] {a}_{k}=(+,-){a}_{n-(k-1)}...k\in[1,2,...,n]](/latexrender/pictures/a0beb8da7f7887762228fcfccee13aad.png)
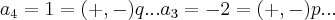
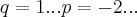
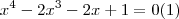
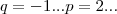
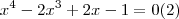

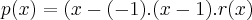


![r=1+\sqrt[4-3]{\left|max.(1,-2,2,1)/1 \right|}=1+\left|2 \right|=3
[-3,3] r=1+\sqrt[4-3]{\left|max.(1,-2,2,1)/1 \right|}=1+\left|2 \right|=3
[-3,3]](/latexrender/pictures/e822c74be605c3716984af7a9b8278a0.png)

