 por adauto martins » Sáb Out 19, 2019 20:40
por adauto martins » Sáb Out 19, 2019 20:40
(escola de aeronautica-exame de admissao 1945)
sabe-se que a secante de um arco do 2° quadrante é -2.calcular o seno e a tangente desse arco.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Out 19, 2019 20:51
por adauto martins » Sáb Out 19, 2019 20:51
soluçao:
![secx=1/cosx=-2\Rightarrow cosx=-1/2\Rightarrow
{senx}^{2}+{cosx}^{2}=1\Rightarrow senx=\sqrt[]{1-{cosx}^{2}} secx=1/cosx=-2\Rightarrow cosx=-1/2\Rightarrow
{senx}^{2}+{cosx}^{2}=1\Rightarrow senx=\sqrt[]{1-{cosx}^{2}}](/latexrender/pictures/55363c90bf3044f228a79efb232d83a3.png)
,
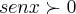
,
pois seg.quadrante...
entao
![senx=\sqrt[]{1-(-1/2)^{2}}=\sqrt[]{3}/2... senx=\sqrt[]{1-(-1/2)^{2}}=\sqrt[]{3}/2...](/latexrender/pictures/ddb376fe4feb5aec67f5ec2abd504bf2.png)
![tgx=senx/cosx=(\sqrt[]{3}/2)/(-1/2)=-\sqrt[]{3}... tgx=senx/cosx=(\sqrt[]{3}/2)/(-1/2)=-\sqrt[]{3}...](/latexrender/pictures/5f9fb04dce323f7d7528bc4f5c17d9c7.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![secx=1/cosx=-2\Rightarrow cosx=-1/2\Rightarrow
{senx}^{2}+{cosx}^{2}=1\Rightarrow senx=\sqrt[]{1-{cosx}^{2}} secx=1/cosx=-2\Rightarrow cosx=-1/2\Rightarrow
{senx}^{2}+{cosx}^{2}=1\Rightarrow senx=\sqrt[]{1-{cosx}^{2}}](/latexrender/pictures/55363c90bf3044f228a79efb232d83a3.png) ,
,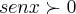 ,
,![senx=\sqrt[]{1-(-1/2)^{2}}=\sqrt[]{3}/2... senx=\sqrt[]{1-(-1/2)^{2}}=\sqrt[]{3}/2...](/latexrender/pictures/ddb376fe4feb5aec67f5ec2abd504bf2.png)
![tgx=senx/cosx=(\sqrt[]{3}/2)/(-1/2)=-\sqrt[]{3}... tgx=senx/cosx=(\sqrt[]{3}/2)/(-1/2)=-\sqrt[]{3}...](/latexrender/pictures/5f9fb04dce323f7d7528bc4f5c17d9c7.png)


 .
.



