 por Gebe » Sex Set 28, 2018 23:01
por Gebe » Sex Set 28, 2018 23:01
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Seg Out 15, 2018 17:18
por ezidia51 » Seg Out 15, 2018 17:18
Olá só passando por aqui para agradecer toda ajuda que vc tem me dado nos exercícios e desejar um Feliz dia dos professores!! Segue anexo um cálculo especial para vc ,meu professor de matemática aqui no fórum.Obrigado por tudo mesmo!!!Abraços!!
- Anexos
-

-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Seg Out 15, 2018 22:26
por Gebe » Seg Out 15, 2018 22:26
Haha gostei! Obrigado por lembrar, é sempre bom poder compartilhar o conhecimento, mais ainda quando há reconhecimento. Bons estudos!

-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Seg Out 15, 2018 22:30
por ezidia51 » Seg Out 15, 2018 22:30
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Sex Out 19, 2018 17:08
por ezidia51 » Sex Out 19, 2018 17:08
Olá vc poderia me ajudar a resolver estes problemas?Como faço este cálculo de parametrização de curvas?
4-Obtenha uma parametrização para a curva de equação geral

Segue possiveis respostas no anexo,mas gostaria de saber como é feito este cálculo.
3-Qual é a melhor representação geométrica do domínio da função ?(Como faço para representar geometricamente o dominio desta função?)
![f(x,y)=\sqrt[2]{y-{x}^{2}} f(x,y)=\sqrt[2]{y-{x}^{2}}](/latexrender/pictures/8af62dc12323ad7dbd37b8bdcad34037.png)
Obrigado
- Anexos
-

-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Sex Out 19, 2018 17:24
por ezidia51 » Sex Out 19, 2018 17:24
Se vc puder dar uma olhada nestes outros exercícios ,eu fico muito agradecida!!
- Anexos
-

-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Sáb Out 20, 2018 00:56
por Gebe » Sáb Out 20, 2018 00:56
Sobre as 3 questões (ultima postagem):
1)
Se formos determinar as superfícies de nível neste caso teremos planos no R³.
Lembrando a equação geral do plano:
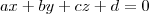
Podemos ver isso achando algumas destas superfícies, veja:

Como podemos ver estas superfícies tem formulação semelhante a eq. geral do plano.
2)
A equação geral de elipses é:
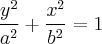
, sendo "a" a ordenada e "b" a abscissa.
O enunciado pede a curva de nivel 4, portanto teremos:

Logo elipse com ordenada 4 e abscissa 3 (Letra E).
3) Nessa não entendi o que está escrito no enunciado "...conjunto dos pontos em que ? ...".
Mas o grafico desta função lembra uma cela de cavalo, pode ver no link abaixo.
https://www.google.com/search?q=x%5E2-y%5E2&client=firefox-b&source=lnms&sa=X&ved=0ahUKEwiMw-W38JPeAhUBgpAKHWqEAxAQ_AUICSgA&biw=1366&bih=650&dpr=1Sobre a outra postagem:
4)
Pela equação é possível identifica-la como uma elipse.
Podemos "arrumar" a equação da seguinte forma:
![\\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\ \\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\](/latexrender/pictures/20ed23358145249fc83094d2baaa0475.png)
Se fizermos a troca:
![\\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\ \\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\](/latexrender/pictures/3caf55b1054e4777fd6e8a1bb38c661f.png)
Ficamos com A² + B² = 1
Podemos ver a semelhança entre essa formulação e a identidade trigonométrica cos²t + sen²t = 1.
Vamos então "forçar" esta semelhança:
![\\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\ \\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\](/latexrender/pictures/655f18a5d5496770aca2866512d6ff38.png)
Resp:
![\gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right) \gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right)](/latexrender/pictures/33fdf4861c71943c19d768a4e85c89ad.png)
3)
Precisamos lembrar que nas funções reais só podemos ter valores maiores ou iguais a zero, logo:
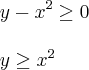
Como podemos ver o domínio da função f(x,y) está acima da parábola y=x².
Como a imagem da função está no R³ e não temos restrições para z, o domínio será então uma "calha" formada por parábolas y=x² ao longo do eixo z.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Sáb Out 20, 2018 23:44
por ezidia51 » Sáb Out 20, 2018 23:44
Um super muito obrigado.Quanto ao exercício que vc não entendeu segue aqui a pergunta:
Considere a função

. Sobre o conjunto dos pontos em que vale , é correto afirmar:
a-é um par de retas que passam pela origem
b-É uma circunferência de centro na origem.
c-Nenhuma das alternativas.
d-É formado por exatamente uma reta.
e-É formado por um único ponto.
Como vc me mostrou no gráfico trata-se de uma hiperbole então a resposta correta aqui seria a letra a?
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Dom Out 21, 2018 01:03
por Gebe » Dom Out 21, 2018 01:03
Agora me pego, realmente não sei o que o enunciado quer dizer com isso, parece que está falando do dominio da função, mas nesse caso a resposta seria "nenhuma das altern", ja que a função está definida para todo R² (todo x e y).
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Dom Out 21, 2018 16:34
por ezidia51 » Dom Out 21, 2018 16:34
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Seg Out 22, 2018 00:07
por ezidia51 » Seg Out 22, 2018 00:07
Olá estou com uma dúvida:Neste exercício da parametrização para a curva 9x^2+5y^2=1 a resposta não seria (nenhuma das alternativas)porque o valor final é
![\frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}} \frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}}](/latexrender/pictures/75bc11fbba7efd7b60797a155deecf34.png)
? (segue anexo o exercício)
- Anexos
-

-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Seg Out 22, 2018 01:02
por Gebe » Seg Out 22, 2018 01:02
Os dois resultados são idênticos, se multiplicar o numerador e o denominador por
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png)
chega-se no formato da alternativa.
![\\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent \\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent](/latexrender/pictures/bcc68a0619e8c851374465ab64d2bec3.png)
Aproveitando, tem só um detalhe que falta no gabarito, o intervalo do parâmetro.
Perceba que para formar a elipse o parâmetro "t" deve estar em um intervalo de 2Pi.
Menos que isso não formamos a elipse e mais que isso começamos a sobrescrever a elipse.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Ter Out 23, 2018 00:12
por ezidia51 » Ter Out 23, 2018 00:12
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Qua Out 24, 2018 22:53
por ezidia51 » Qua Out 24, 2018 22:53
Olá vc poderia me ajudar com estes problemas de duas variáveis?Segue anexo as fotos (onde coloquei o x é a resposta mas acho que está errada).Obrigada
- Anexos
-

-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Qua Out 24, 2018 22:54
por ezidia51 » Qua Out 24, 2018 22:54
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Qua Out 24, 2018 22:57
por ezidia51 » Qua Out 24, 2018 22:57
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Qui Out 25, 2018 04:15
por Gebe » Qui Out 25, 2018 04:15
Continuidade/Limites com multiplas variaveis pode ser consideravelmente mais complicado. Por exemplo, não temos a facilidade da regra de l'Hopital.
Por esse motivo, temos dois tipos comuns de questões, um no qual temos que primeiro simplificar a função de alguma forma e outra onde tentamos mostrar que o limite não existe.
Lembrando: para que seja continua em (2,2), f(2,2) = lim[2,2] f(x,y), ou seja:
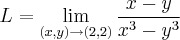
Se fizermos a simples substituição dos valores dados (2,2), temos uma indeterminação 0/0.
Nesta questão (6) temos um exemplo de questão que a simplicação pode ser feita.
Podemos tentar dividir o polinomio do denominador pelo polinomio do numerador, já que o denominador tem ordem maior.
Essa divisão dará como resultado:
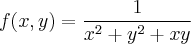
Perceba que agora a indeterminação não existe mais e o limite vale 1/12. (Nenhuma das alternativas).
Quanto as questões 4 e 5. Não acho que as restrições no dominio tenham efeito na resposta.
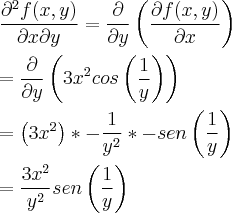
Resp: Nenhuma das alternativas
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Qui Out 25, 2018 13:55
por ezidia51 » Qui Out 25, 2018 13:55
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Maisa_Rany » Ter Nov 06, 2018 21:13
por Maisa_Rany » Ter Nov 06, 2018 21:13
Boa noite!
Como ficou a resposta final?
Obrigada!
-
Maisa_Rany
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Out 25, 2018 20:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por ezidia51 » Seg Nov 26, 2018 09:23
por ezidia51 » Seg Nov 26, 2018 09:23
Bom dia!!Você poderia dar uma olhada nestes exercícios que eu fiz de cálculo 2.Tenho dúvidas nas questões 1 e 3.Se você puder me ajudar ficarei muito agradecida.Obrigado Ezidia
- Anexos
-

-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Seg Nov 26, 2018 09:25
por ezidia51 » Seg Nov 26, 2018 09:25
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por ezidia51 » Seg Nov 26, 2018 09:29
por ezidia51 » Seg Nov 26, 2018 09:29
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Qua Nov 28, 2018 16:15
por Gebe » Qua Nov 28, 2018 16:15
1) certa.
O solido é este -->
https://academo.org/demos/3d-surface-plotter/?expression=2*x*y&xRange=1%2C4&yRange=0%2C2&resolution=252)Errada.
A area certa é esta:
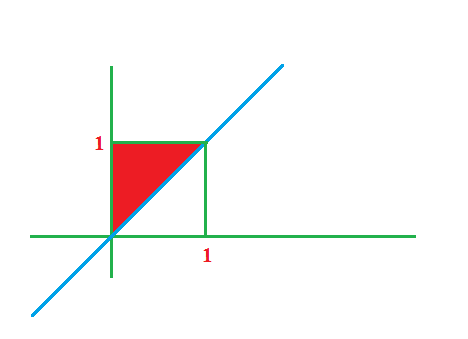
- fd.png (4.99 KiB) Exibido 48111 vezes
Assim, quando fazemos a troca das variaveis fica:
x ? y ? 1
0 ? x ? 1
Letra C
3) certa, Letra C
A area é esta:
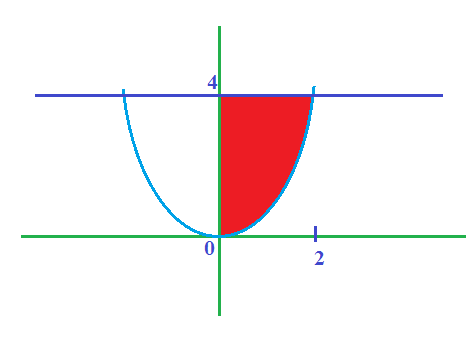
- Sem título.png (5.5 KiB) Exibido 48111 vezes
4)Errada
Aqui tu considerou apenas metade da area, veja:
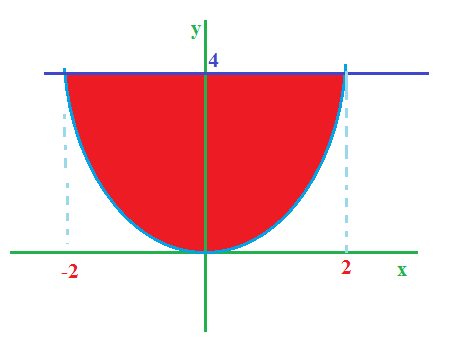
- 4.png (6.48 KiB) Exibido 48111 vezes
Logo teremos:
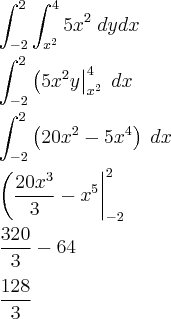
5) certa
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Qua Nov 28, 2018 20:35
por ezidia51 » Qua Nov 28, 2018 20:35
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Qui Nov 29, 2018 18:37
por Gebe » Qui Nov 29, 2018 18:37
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por dark_slack » Qui Dez 13, 2018 22:59
por dark_slack » Qui Dez 13, 2018 22:59
Boa noite fórum, tenho um problema de derivada parcial que não consigo resolver e peço a atenção de vocês para me ajudarem.
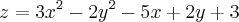
, descobrir a tangente que intercepta f(x, y) com y = 2 no ponto (1, 2, -3).
-
dark_slack
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Dez 13, 2018 19:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por ezidia51 » Seg Dez 24, 2018 16:34
por ezidia51 » Seg Dez 24, 2018 16:34
Olá Gebe!!
Hoje não estou aqui para pedir nenhuma ajuda matemática ,mas sim para agradecer por toda ajuda que você tem me dado nos exercícios que tenho que estudar!!Estou fazendo Licenciatura em Matemática e felizmente consegui passar na prova de cálculo 2 .Graças a sua ajuda e muito estudo, consegui vencer mais uma etapa. Muito obrigado mesmo.Nesta data especial,desejo a você e a sua família um super feliz Natal e um Ano Novo repleto de realizações!Feliz 2019!!!

- Anexos
-

-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Ter Dez 25, 2018 17:06
por Gebe » Ter Dez 25, 2018 17:06
HoHoHo Feliz Natal!

Obrigado pela mensagem.

Desejo a ti e a tua família o mesmo.

-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Ter Dez 25, 2018 19:06
por ezidia51 » Ter Dez 25, 2018 19:06
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema basico de fisica usando derivadas
 por iksin » Ter Set 11, 2018 16:29
por iksin » Ter Set 11, 2018 16:29
- 1 Respostas
- 7399 Exibições
- Última mensagem por Gebe

Ter Set 11, 2018 17:38
Cálculo: Limites, Derivadas e Integrais
-
- Maximo e minimo usando derivadas parciais
por duduxo81 » Seg Nov 27, 2017 19:55
- 0 Respostas
- 4464 Exibições
- Última mensagem por duduxo81

Seg Nov 27, 2017 19:55
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas - Problemas
por cassiog » Ter Mai 18, 2010 18:48
- 0 Respostas
- 4651 Exibições
- Última mensagem por cassiog

Ter Mai 18, 2010 18:48
Cálculo: Limites, Derivadas e Integrais
-
- Problemas de derivadas
por paolaads » Seg Nov 07, 2011 21:34
- 7 Respostas
- 11946 Exibições
- Última mensagem por LuizAquino

Sáb Dez 03, 2011 14:37
Cálculo: Limites, Derivadas e Integrais
-
- Intergral da Sec(x) dx usando tg(x/2)=Z
por rycherr » Ter Mai 08, 2012 01:32
- 3 Respostas
- 3710 Exibições
- Última mensagem por LuizAquino

Ter Mai 08, 2012 17:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









![f(x,y)=\sqrt[2]{y-{x}^{2}} f(x,y)=\sqrt[2]{y-{x}^{2}}](/latexrender/pictures/8af62dc12323ad7dbd37b8bdcad34037.png)


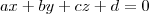

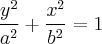 , sendo "a" a ordenada e "b" a abscissa.
, sendo "a" a ordenada e "b" a abscissa.
![\\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\ \\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\](/latexrender/pictures/20ed23358145249fc83094d2baaa0475.png)
![\\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\ \\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\](/latexrender/pictures/3caf55b1054e4777fd6e8a1bb38c661f.png)
![\\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\ \\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\](/latexrender/pictures/655f18a5d5496770aca2866512d6ff38.png)
![\gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right) \gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right)](/latexrender/pictures/33fdf4861c71943c19d768a4e85c89ad.png)
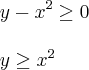

 . Sobre o conjunto dos pontos em que vale , é correto afirmar:
. Sobre o conjunto dos pontos em que vale , é correto afirmar:





 Muito muito obrigado !!!
Muito muito obrigado !!!
![\frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}} \frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}}](/latexrender/pictures/75bc11fbba7efd7b60797a155deecf34.png) ? (segue anexo o exercício)
? (segue anexo o exercício)
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) chega-se no formato da alternativa.
chega-se no formato da alternativa.![\\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent \\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent](/latexrender/pictures/bcc68a0619e8c851374465ab64d2bec3.png)









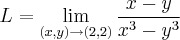
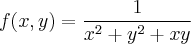
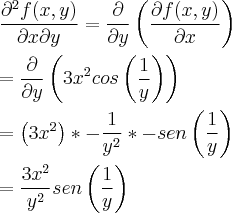





 Um super muito obrigado!!!Agora me esclareceu um pouco .Valeu mesmo!!!!
Um super muito obrigado!!!Agora me esclareceu um pouco .Valeu mesmo!!!!





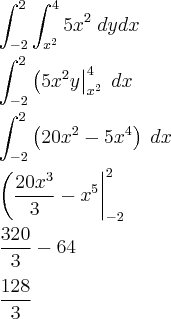








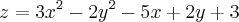 , descobrir a tangente que intercepta f(x, y) com y = 2 no ponto (1, 2, -3).
, descobrir a tangente que intercepta f(x, y) com y = 2 no ponto (1, 2, -3).









 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
