








![f(x,y)=\sqrt[2]{y-{x}^{2}} f(x,y)=\sqrt[2]{y-{x}^{2}}](/latexrender/pictures/8af62dc12323ad7dbd37b8bdcad34037.png)


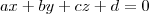

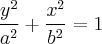 , sendo "a" a ordenada e "b" a abscissa.
, sendo "a" a ordenada e "b" a abscissa.
![\\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\ \\
9x^2+5y^2=1\\
\\
\frac{x^2}{\frac{1}{3^2}}+\frac{y^2}{\frac{1}{\sqrt[]{5}^2}}=1\\
\\
\left(\frac{x}{\frac{1}{3}} \right)^2+\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2=1\\
\\](/latexrender/pictures/20ed23358145249fc83094d2baaa0475.png)
![\\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\ \\
A^2=\left(\frac{x}{\frac{1}{3}} \right)^2\\
B^2 =\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)^2
\\](/latexrender/pictures/3caf55b1054e4777fd6e8a1bb38c661f.png)
![\\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\ \\
A^2 = cos^2t\\
A = cos\;t\\
\left(\frac{x}{\frac{1}{3}} \right)=cos\;t\\
\\
x = \frac{1}{3}cos\;t\\
\\
\\
B^2 = sen^2t\\
B = sen\;t\\
\left(\frac{y}{\frac{1}{\sqrt[]{5}}} \right)=sen\;t\\
\\
y = \frac{1}{\sqrt[]{5}}sen\;t\\](/latexrender/pictures/655f18a5d5496770aca2866512d6ff38.png)
![\gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right) \gamma(t) = \left(\frac{1}{3}cos\;t\;,\;\frac{\sqrt[]{5}}{5}sen\;t \right)](/latexrender/pictures/33fdf4861c71943c19d768a4e85c89ad.png)
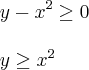

 . Sobre o conjunto dos pontos em que vale , é correto afirmar:
. Sobre o conjunto dos pontos em que vale , é correto afirmar:





 Muito muito obrigado !!!
Muito muito obrigado !!!
![\frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}} \frac{1}{3}cos(t),\frac{1}{\sqrt[]{5}}](/latexrender/pictures/75bc11fbba7efd7b60797a155deecf34.png) ? (segue anexo o exercício)
? (segue anexo o exercício)
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) chega-se no formato da alternativa.
chega-se no formato da alternativa.![\\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent \\
\frac{1}{\sqrt[]{5}}sent\\
\\
\frac{1}{\sqrt[]{5}}sent*\frac{\sqrt[]{5}}{\sqrt[]{5}}\\
\\
\frac{\sqrt[]{5}}{\left(\sqrt[]{5} \right)^2}sent\\
\\
\frac{\sqrt[]{5}}{5}sent](/latexrender/pictures/bcc68a0619e8c851374465ab64d2bec3.png)









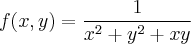
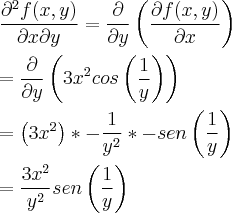





 Um super muito obrigado!!!Agora me esclareceu um pouco .Valeu mesmo!!!!
Um super muito obrigado!!!Agora me esclareceu um pouco .Valeu mesmo!!!!





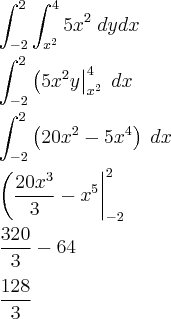








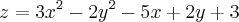 , descobrir a tangente que intercepta f(x, y) com y = 2 no ponto (1, 2, -3).
, descobrir a tangente que intercepta f(x, y) com y = 2 no ponto (1, 2, -3).







Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.