
Estou estudando para um concurso e me deparei com uma questão que me deixou em dúvida! Espero que possam me ajudar!
A questão é a seguinte:
Resolva a seguinte inequação em R (reais) e responda na forma de intervalo:
1/x²-1 < 1/x³-1 (1 sobre x²-1 menor que 1 sobre x³-1)
Minha resolução:
Eu passei a parte igualada para o lado esquerdo e ficou assim: 1/x²-1 - (1/x³-1) < 0
Tirando o mmc: x³-1 - (x²-1)/ (x²-1)(x³-1)< 0
Simplificando: x³-x² / (x²-1)(x³-1)< 0
Decompus o denominador e o primeiro termo do numerador: x²(x-1) / (x+1)(x-1)(x³-1)< 0
Anulei (x-1) embaixo e em cima: x² / (x+1)(x³-1)< 0
Eu fiz o quadro de sinais e a resposta na forma de intervalo ficou: [0,1]
Mas acho que está errado, devo ter errado algo na resolução.
Peço que me ajudem.


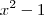 :
:

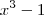 :
: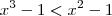

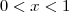 e
e 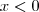



 ou
ou 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)