 por Paloma » Ter Mar 16, 2010 21:06
por Paloma » Ter Mar 16, 2010 21:06
minha dificuldade não é em limites propriamente, mas na fatoração de polinômios, quando tendem a zero, ou acabam em uma indeterinação

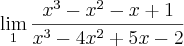
como nesse caso, vai dá um indeterminação,

.. eu queria ajuda na fatoração, se alguém poder ajudar

brigada
-
Paloma
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mar 16, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Ter Mar 16, 2010 21:51
por MarceloFantini » Ter Mar 16, 2010 21:51
Boa noite.
Paloma, tentou usar a regra de L'Hospital?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Paloma » Ter Mar 16, 2010 22:12
por Paloma » Ter Mar 16, 2010 22:12
eu consegui, dividindo os polinômios.. não conheço a regra de L'Hospital, mas vou pesquisar, tavez me ajude nas próximas

brigada

-
Paloma
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mar 16, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em Engenharia Civil
- Andamento: cursando
 por Molina » Ter Mar 16, 2010 22:15
por Molina » Ter Mar 16, 2010 22:15
Também acho mais fácil usar L'Hopital do que procurar fatorar aquelas duas coisas ali.
SÓ QUE...
Quando você começa ver limites não tem derivadas ainda.
Então temos que ver qual o estágio da Paloma.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Paloma » Ter Mar 16, 2010 22:23
por Paloma » Ter Mar 16, 2010 22:23
tô no primeiro período, não tem derivada ainda
-
Paloma
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mar 16, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em Engenharia Civil
- Andamento: cursando
 por Elcioschin » Ter Mar 16, 2010 22:55
por Elcioschin » Ter Mar 16, 2010 22:55
A fatoração, neste caso é bem simples
Numerador ----> (x³ - x²) - (x - 1) = x²*(x - 1) - (x - 1) = (x² - 1)*(x - 1) = (x + 1)*(x - 1)²
Para haver uma eventual simplificação devemos verificar as raízes x = -1 e x = +1 no denominador. Briott-Ruffini:
___|.. +1 .... -4 ..... +5 ...... -2 .....
+1.|.. +1 .... -3 ...... +2 ...... 0 ...... ----> +1 é raiz
+1.|.. +1 .... -2 ....... 0 ............... ----> +1 é outra raiz
+2.|.. +1 ..... 0 ......................... ----> +2 é raiz
(x³ - x² - x + 1)/(x³ - 4x² + 5x - 1) = (x + 1)*(x - 1)²/(x - 2)((x - 1)² = (x + 1)/(x - 2)
Para x ---> 1 ------> Limite ----> - 2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Paloma » Qua Mar 17, 2010 11:11
por Paloma » Qua Mar 17, 2010 11:11
numa questão como essa por exemplo,
![\lim_{-1} \frac{\sqrt[2]{3{t}^{2}+1}-2}{2\left(t+1 \right)} \lim_{-1} \frac{\sqrt[2]{3{t}^{2}+1}-2}{2\left(t+1 \right)}](/latexrender/pictures/ce2de3cb1c3fcf7634d13fac1111dc3b.png)
pra tirar o radical, multiplica pela conjugada certo? mas chega num ponto que eu não se mais o que fazer..
alguém sabe uma forma simple pra simpificar tudo iss ae? pra não dá em uma indeterminação..
brigada

-
Paloma
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mar 16, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em Engenharia Civil
- Andamento: cursando
 por Elcioschin » Qua Mar 17, 2010 13:18
por Elcioschin » Qua Mar 17, 2010 13:18
Multiplicando pelo conjugado:
[V(3t² + 1) - 2]*[V(3t² + 1) + 2]/2*(t + 1)*[V(3t² + 1) + 2] = [(3t² + 1) - 2²]/2*(t + 1)*[V(3t² + 1) + 2] =
(3t² - 3)/2*(t + 1)*[V(3t² + 1) + 2] = 3*(t² - 1)/2*(t + 1)*[V(3t² + 1) + 2] = 3*(t + 1)*(t - 1)/2*(t + 1)*[V(3t² + 1) + 2]
Simplificando (t + 1):
= 3*(t - 1)/2*[V(3t² + 1) + 2] ---> Fazendo t = -1:
= 3(- 1 - 1)/2*{V[3*(-1)² + 1] + 2} = 3*(-2)/(2*4) = - 3/4
Editado pela última vez por
Elcioschin em Qua Mar 17, 2010 18:15, em um total de 1 vez.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Paloma » Qua Mar 17, 2010 14:48
por Paloma » Qua Mar 17, 2010 14:48
depois de muitas tentativas eu consegui multiplicando pelo conjugado, Elcioschin, do mesmo jeito que você fez.. mas meu resultado final deu -3/4
![\lim_{-1} \frac{3t-3}{2\sqrt[2]{3{t}^{2}+1}+2} \lim_{-1} \frac{3t-3}{2\sqrt[2]{3{t}^{2}+1}+2}](/latexrender/pictures/00ad12a882a3a4c364b9e658ec392879.png)
substituindo t por -1;
![\lim_{-1} \frac{3.(-1)-3}{2\sqrt[2]{3.{-1}^{2}+1}+2} \lim_{-1} \frac{3.(-1)-3}{2\sqrt[2]{3.{-1}^{2}+1}+2}](/latexrender/pictures/90f1e7d9c0fedf76da1ebaabf5afa2d2.png)
=

eu susbtituí errado?
-
Paloma
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mar 16, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em Engenharia Civil
- Andamento: cursando
 por Elcioschin » Qua Mar 17, 2010 18:15
por Elcioschin » Qua Mar 17, 2010 18:15
Erro meu de soma na última linha: já corrigí.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Paloma » Sáb Mar 20, 2010 13:57
por Paloma » Sáb Mar 20, 2010 13:57
Alguém poderia me ajudar a terminar essa questão?

->
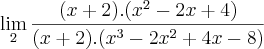
elimino (x+2) com (x+2),
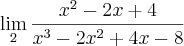
e não sei mais como continuar.
-
Paloma
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mar 16, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Indeterminação
 por Aliocha Karamazov » Sex Nov 25, 2011 00:28
por Aliocha Karamazov » Sex Nov 25, 2011 00:28
- 2 Respostas
- 1948 Exibições
- Última mensagem por Aliocha Karamazov

Sex Nov 25, 2011 21:21
Cálculo: Limites, Derivadas e Integrais
-
- Limite indeterminação 0/0
por ravi » Ter Mai 08, 2012 06:42
- 1 Respostas
- 1378 Exibições
- Última mensagem por LuizAquino

Ter Mai 08, 2012 12:13
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida: Limite com indeterminação 0/0
por Samira » Sáb Nov 27, 2010 20:04
- 3 Respostas
- 3337 Exibições
- Última mensagem por andrefahl

Dom Nov 28, 2010 00:06
Cálculo: Limites, Derivadas e Integrais
-
- [Limite no infinito]casos de indeterminação
por moyses » Sex Set 09, 2011 00:24
- 9 Respostas
- 5663 Exibições
- Última mensagem por LuizAquino

Seg Set 12, 2011 12:18
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo de limite] quando há indeterminação 0/0
por JessicaDias » Qui Abr 12, 2012 20:00
- 2 Respostas
- 2992 Exibições
- Última mensagem por JessicaDias

Qui Abr 12, 2012 21:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

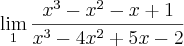
 .. eu queria ajuda na fatoração, se alguém poder ajudar
.. eu queria ajuda na fatoração, se alguém poder ajudar 


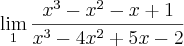
 .. eu queria ajuda na fatoração, se alguém poder ajudar
.. eu queria ajuda na fatoração, se alguém poder ajudar 









![\lim_{-1} \frac{\sqrt[2]{3{t}^{2}+1}-2}{2\left(t+1 \right)} \lim_{-1} \frac{\sqrt[2]{3{t}^{2}+1}-2}{2\left(t+1 \right)}](/latexrender/pictures/ce2de3cb1c3fcf7634d13fac1111dc3b.png)



![\lim_{-1} \frac{3t-3}{2\sqrt[2]{3{t}^{2}+1}+2} \lim_{-1} \frac{3t-3}{2\sqrt[2]{3{t}^{2}+1}+2}](/latexrender/pictures/00ad12a882a3a4c364b9e658ec392879.png)
![\lim_{-1} \frac{3.(-1)-3}{2\sqrt[2]{3.{-1}^{2}+1}+2} \lim_{-1} \frac{3.(-1)-3}{2\sqrt[2]{3.{-1}^{2}+1}+2}](/latexrender/pictures/90f1e7d9c0fedf76da1ebaabf5afa2d2.png) =
= 


 ->
->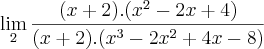
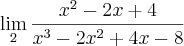

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
