 por ezidia51 » Seg Mar 12, 2018 23:39
por ezidia51 » Seg Mar 12, 2018 23:39
1) LaTeX: \frac{\sqrt{20}}{\sqrt{810}}
![\sqrt[]{}\frac{20}{810} \sqrt[]{}\frac{20}{810}](/latexrender/pictures/0b07cccca8c469e9fa169ec9453d92bc.png)
então fatorei o 20 e o 810 20=2.5 e o 810 =2.3^4.5 e aí me perdi.Não sei se resolvo o que está dentro da raiz ou se elimino os numeros 2 e 5.
2)] LaTeX: x\text{ }\sqrt[3]{(x^2 )}+5x^{\frac{5}{3}}-6\sqrt[3]{x^5= x .
![x.{x}^{\frac{2}{3}}+5\sqrt[3]{x^5}-6\sqrt[3]{x^5} x.{x}^{\frac{2}{3}}+5\sqrt[3]{x^5}-6\sqrt[3]{x^5}](/latexrender/pictures/b4b0a2cc497baedd65632d3067c28ddc.png)
e aí não consegui mais desenvolver o raciocinio.Acho que tem algo errado.
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
 por Gebe » Ter Mar 13, 2018 01:26
por Gebe » Ter Mar 13, 2018 01:26
1)
![\sqrt[2]{\frac{20}{810}} = \sqrt[2]{\frac{2*2*5}{2*3*3*3*3*5}}=\sqrt[2]{\frac{2}{3^2*3^2}}=\frac{1}{3*3}\sqrt[2]{2}=\frac{1}{9}\sqrt[2]{2} \sqrt[2]{\frac{20}{810}} = \sqrt[2]{\frac{2*2*5}{2*3*3*3*3*5}}=\sqrt[2]{\frac{2}{3^2*3^2}}=\frac{1}{3*3}\sqrt[2]{2}=\frac{1}{9}\sqrt[2]{2}](/latexrender/pictures/4653802606e42e968097231db4178af8.png)
Perceba que os numeros com expoentes
multiplos do indice da raiz podem ser simplificados, ou seja, podemos "retirar" estes termos da raiz.
Fica facil de ver se colocarmos os termos com expoentes fracionarios, como é feito na questao 2.
2)
Essa questao, como mencionado antes, fica simples se colocarmos os termos com expoente fracionado. Perceba tambem que utilizamos uma propriedade que diz:
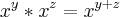
.
![x\text{ }\sqrt[3]{(x^2 )}+5x^{\frac{5}{3}}-6\sqrt[3]{x^5}=x*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}=x^\frac{3}{3}*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}= x\text{ }\sqrt[3]{(x^2 )}+5x^{\frac{5}{3}}-6\sqrt[3]{x^5}=x*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}=x^\frac{3}{3}*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}=](/latexrender/pictures/ddd555ec8055f53899256b70488701aa.png)
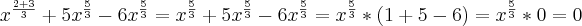
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ezidia51 » Ter Mar 13, 2018 12:21
por ezidia51 » Ter Mar 13, 2018 12:21
-
ezidia51
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mar 12, 2018 20:57
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em enfermagem
- Andamento: formado
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplificação de raizes
por LuizCarlos » Sáb Mai 05, 2012 00:14
- 3 Respostas
- 2328 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 14:00
Álgebra Elementar
-
- Simplificação de raízes.
por Sobreira » Qui Mai 09, 2013 22:21
- 1 Respostas
- 1318 Exibições
- Última mensagem por brunnkpol

Qui Mai 09, 2013 23:49
Aritmética
-
- [simplificação de expressoes] eliminar raizes
por bira19 » Qui Out 06, 2011 23:33
- 2 Respostas
- 2443 Exibições
- Última mensagem por bira19

Dom Out 09, 2011 17:47
Álgebra Elementar
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2354 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8120 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{}\frac{20}{810} \sqrt[]{}\frac{20}{810}](/latexrender/pictures/0b07cccca8c469e9fa169ec9453d92bc.png) então fatorei o 20 e o 810 20=2.5 e o 810 =2.3^4.5 e aí me perdi.Não sei se resolvo o que está dentro da raiz ou se elimino os numeros 2 e 5.
então fatorei o 20 e o 810 20=2.5 e o 810 =2.3^4.5 e aí me perdi.Não sei se resolvo o que está dentro da raiz ou se elimino os numeros 2 e 5.![x.{x}^{\frac{2}{3}}+5\sqrt[3]{x^5}-6\sqrt[3]{x^5} x.{x}^{\frac{2}{3}}+5\sqrt[3]{x^5}-6\sqrt[3]{x^5}](/latexrender/pictures/b4b0a2cc497baedd65632d3067c28ddc.png) e aí não consegui mais desenvolver o raciocinio.Acho que tem algo errado.
e aí não consegui mais desenvolver o raciocinio.Acho que tem algo errado.

![\sqrt[2]{\frac{20}{810}} = \sqrt[2]{\frac{2*2*5}{2*3*3*3*3*5}}=\sqrt[2]{\frac{2}{3^2*3^2}}=\frac{1}{3*3}\sqrt[2]{2}=\frac{1}{9}\sqrt[2]{2} \sqrt[2]{\frac{20}{810}} = \sqrt[2]{\frac{2*2*5}{2*3*3*3*3*5}}=\sqrt[2]{\frac{2}{3^2*3^2}}=\frac{1}{3*3}\sqrt[2]{2}=\frac{1}{9}\sqrt[2]{2}](/latexrender/pictures/4653802606e42e968097231db4178af8.png)
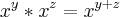 .
.![x\text{ }\sqrt[3]{(x^2 )}+5x^{\frac{5}{3}}-6\sqrt[3]{x^5}=x*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}=x^\frac{3}{3}*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}= x\text{ }\sqrt[3]{(x^2 )}+5x^{\frac{5}{3}}-6\sqrt[3]{x^5}=x*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}=x^\frac{3}{3}*x^\frac{2}{3}+5x^{\frac{5}{3}}-6x^\frac{5}{3}=](/latexrender/pictures/ddd555ec8055f53899256b70488701aa.png)
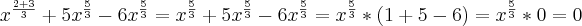


 , avisa que eu resolvo.
, avisa que eu resolvo.

