 por irineu junior » Sex Mar 12, 2010 20:57
por irineu junior » Sex Mar 12, 2010 20:57
Boa noite, vou fazer uma prova semana que vem, e uma das materias que vai cair é Função inversa, cujo eu nunca ouvi falar, poderiam me dar alguns exemplos e resoluções, obrigado
-
irineu junior
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Mar 12, 2010 20:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Elcioschin » Dom Mar 14, 2010 14:23
por Elcioschin » Dom Mar 14, 2010 14:23
irineu
O assunto é simples porém vasto.
Fica complicado explicar no fórum toda a teoria sobre o assunto.
Sem a teoria vc não vai entender bem o assunto
Sugiro que vc dê uma estudada na teoria em qualquer livro do Ensino Médio (Funções). Se vc não possuir livro ou apostila, sugiro procurar na internet: Google - Funções - Funções inversas.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por irineu junior » Dom Mar 14, 2010 16:28
por irineu junior » Dom Mar 14, 2010 16:28
Ok valeu a dica, conheci algumas formas de encontrar a função inversa, porém as que vi são simples, fazendo crer que é um assunto banal.
Gostaria da resolução do exercicio a seguir.
A função
![y=f(x)=\sqrt[]{x+1} y=f(x)=\sqrt[]{x+1}](/latexrender/pictures/63166e6fd5fea7bffa2672c17a5bb884.png)
, a inversa
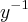
dessa função é:
A=
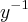
=
![\sqrt[]{y-1} \sqrt[]{y-1}](/latexrender/pictures/a245d038b5a69b4b333b28c8655c2fa5.png)
B=
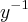
=
![\sqrt[]{y+1} \sqrt[]{y+1}](/latexrender/pictures/a0b8abc31d8021e2af9cd98191fe14de.png)
C=
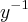
=

+1
D=
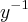
=

-1
E=
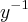
=

+y
segundo o gabarito a resposta correta é a alternativa D.
-
irineu junior
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Mar 12, 2010 20:37
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- função inversa
por gisa123 » Qui Ago 28, 2008 17:22
- 1 Respostas
- 3395 Exibições
- Última mensagem por Molina

Qui Ago 28, 2008 23:53
Funções
-
- Função Inversa
por OtavioBonassi » Qui Jul 14, 2011 23:04
- 6 Respostas
- 7720 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:14
Funções
-
- Função Inversa.
por jcvalim » Qua Ago 24, 2011 15:57
- 0 Respostas
- 1181 Exibições
- Última mensagem por jcvalim

Qua Ago 24, 2011 15:57
Funções
-
- função inversa
por tigre matematico » Qui Out 13, 2011 12:45
- 1 Respostas
- 2206 Exibições
- Última mensagem por Guill

Sáb Abr 21, 2012 18:07
Funções
-
- Função Inversa
por Rafael16 » Qua Mar 14, 2012 12:08
- 3 Respostas
- 1970 Exibições
- Última mensagem por LuizAquino

Qua Mar 14, 2012 15:16
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![y=f(x)=\sqrt[]{x+1} y=f(x)=\sqrt[]{x+1}](/latexrender/pictures/63166e6fd5fea7bffa2672c17a5bb884.png) , a inversa
, a inversa 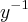 dessa função é:
dessa função é: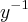 =
=![\sqrt[]{y-1} \sqrt[]{y-1}](/latexrender/pictures/a245d038b5a69b4b333b28c8655c2fa5.png)
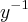 =
=![\sqrt[]{y+1} \sqrt[]{y+1}](/latexrender/pictures/a0b8abc31d8021e2af9cd98191fe14de.png)
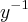 =
= +1
+1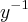 =
= -1
-1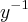 =
= +y
+y