Então, ola a todos, queria pedir ajuda em um exercicio, na verdade dois, mais são quase iguais.
vamos lá...
Hoje a professora passou igualdade de números complexos: 2 números complexos são iguais quando suas partes reais e imaginarias forem respectivamente iguais.
a + bi = c + di / a = c / b = d
Ele deu um ex: Determine x e y de modo que (2x + y) + 6i = 5 + (x + 4y)i
2x + y = 5
6 = x + 4y Então ele passou o jeito 'substituição' para calcular
2x + y = 5 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ y = [5 - 2x] espera
x + 4y = 6 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~y = 5 - 2.2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~y = 5 - 4 = 1
x + 4y = 6 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~Solução = {2 , 1}
x + 4.(5 - 2x) = 6
x + 20 - 8x = 6
x - 8x = 6 - 20
-7x = -14
x = -14/-7 = 2
Então ela passou 2 exercicios, só que eles tem digamos tem menos letras, ou numeros nao sei e nao estou sabendo como fazer.
1_ Determine o valor de a e b de modo que se tenha a - bi = 5 + 2i.
Eu tentei com o formula do exemplo, mais ficou estranho, e tambem tentei trocar a letras por numeros mais ai seria facil demais
2_ Dados z1= (x+y) + 10i e z2 = 16 + (x - y)i obtenha os valores de x e y para que z1 = z2.
Essa eu nao sei como juntalos de forma correta
Alguem poderia me ajudar a resolvelos?
Obrigado


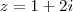 , estamos na verdade definindo um
, estamos na verdade definindo um  , então obrigatoriamente:
, então obrigatoriamente:




 ).
).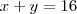

 e
e  .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.