Em geral, apenas enunciados de exercícios.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por DonTLie » Qui Mar 11, 2010 17:23
por DonTLie » Qui Mar 11, 2010 17:23
Então, ola a todos, queria pedir ajuda em um exercicio, na verdade dois, mais são quase iguais.
vamos lá...
Hoje a professora passou igualdade de números complexos: 2 números complexos são iguais quando suas partes reais e imaginarias forem respectivamente iguais.
a + bi = c + di / a = c / b = d
Ele deu um ex: Determine x e y de modo que (2x + y) + 6i = 5 + (x + 4y)i
2x + y = 5
6 = x + 4y Então ele passou o jeito 'substituição' para calcular
2x + y = 5 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ y = [5 - 2x] espera
x + 4y = 6 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~y = 5 - 2.2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~y = 5 - 4 = 1
x + 4y = 6 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~Solução = {2 , 1}
x + 4.(5 - 2x) = 6
x + 20 - 8x = 6
x - 8x = 6 - 20
-7x = -14
x = -14/-7 = 2
Então ela passou 2 exercicios, só que eles tem digamos tem menos letras, ou numeros nao sei e nao estou sabendo como fazer.
1_ Determine o valor de a e b de modo que se tenha a - bi = 5 + 2i.
Eu tentei com o formula do exemplo, mais ficou estranho, e tambem tentei trocar a letras por numeros mais ai seria facil demais
2_ Dados z1= (x+y) + 10i e z2 = 16 + (x - y)i obtenha os valores de x e y para que z1 = z2.
Essa eu nao sei como juntalos de forma correta
Alguem poderia me ajudar a resolvelos?
Obrigado
-
DonTLie
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 09, 2010 20:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Mar 11, 2010 17:55
por MarceloFantini » Qui Mar 11, 2010 17:55
Boa tarde.
Não tem fórmula nenhuma, o que a sua professora quer dizer é o seguinte: para que um número complexo seja igual a outro,
a parte real do primeiro deve ser igual a do segundo, e a parte imaginária idem.
Acredito que a maneira mais fácil de perceber o porque é: quando escrevemos um número complexo
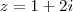
, estamos na verdade definindo um
ponto (ou afixo) no plano de Argand-Gauss, cujas coordenadas são
(1,2). Portanto, para que você tenha um ponto idêntico a esse, devemos ter as mesmas coordenadas, que significam a parte real e imaginária do complexo.
Assim, no primeiro exercício: se

, então obrigatoriamente:


Se você conseguiu entender o conceito, fica fácil resolver o segundo.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DonTLie » Qui Mar 11, 2010 19:43
por DonTLie » Qui Mar 11, 2010 19:43
Obrigado pela ajuda Fantini, eu tinha pensado em fazer dessa forma, pensei que deveria seguir + - o exemplo, agora ficou facil, vlw ae

-
DonTLie
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 09, 2010 20:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DonTLie » Sex Mar 12, 2010 16:37
por DonTLie » Sex Mar 12, 2010 16:37
No exercicio 2, o x e y do z1 tem que ser igual a do z2? se for nao to consiguindo achar os numeros que encaxem
-
DonTLie
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 09, 2010 20:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sex Mar 12, 2010 17:40
por MarceloFantini » Sex Mar 12, 2010 17:40
Lembre-se que a parte real é um número sozinho, e a parte imaginária é um número REAL acompanhado da unidade imaginária (

).
No segundo exercício temos:
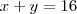

De onde sai que

e

.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Tópicos sem Interação (leia as regras)
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda exercício de matemática números complexos?
por MMSR29 » Qui Jul 24, 2014 22:52
- 7 Respostas
- 9012 Exibições
- Última mensagem por adauto martins

Sáb Nov 01, 2014 15:34
Números Complexos
-
- [Igualdade de Euler] Trigonometria e Complexos
por clecio » Ter Ago 16, 2011 20:56
- 1 Respostas
- 2632 Exibições
- Última mensagem por MarceloFantini

Qua Set 21, 2011 22:14
Números Complexos
-
- [Números complexos] Dúvida
por iceman » Qui Mai 10, 2012 18:52
- 5 Respostas
- 3737 Exibições
- Última mensagem por fraol

Qui Mai 10, 2012 21:15
Números Complexos
-
- Números Complexos - Dúvida
por iceman » Ter Mai 15, 2012 20:22
- 1 Respostas
- 1806 Exibições
- Última mensagem por fraol

Ter Mai 15, 2012 22:20
Números Complexos
-
- Dúvida - Números complexos
por Danilo » Sex Ago 03, 2012 02:05
- 5 Respostas
- 3842 Exibições
- Última mensagem por Danilo

Sex Ago 03, 2012 16:46
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


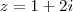 , estamos na verdade definindo um
, estamos na verdade definindo um  , então obrigatoriamente:
, então obrigatoriamente:




 ).
).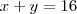

 e
e  .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.