 por pedro22132938 » Sex Dez 30, 2016 01:28
por pedro22132938 » Sex Dez 30, 2016 01:28
O exercicio pede o calculo da integral de linha onde,
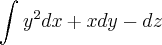
e

é a poligonal de vértices A0 = (0,0,0), A1=(1,1,1) e A2=(1,1,0), orientada de A0 para A2.
Parametrizei a curva gama, mas ao calcular a integral por partes, cheguei ao resultado 0, porém ao verificar a solução está 5/6. Alguém consegue chegar ao resultado e mostrar-me como?
-
pedro22132938
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Mar 22, 2015 17:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: EAD
- Andamento: formado
 por adauto martins » Dom Jan 01, 2017 14:32
por adauto martins » Dom Jan 01, 2017 14:32
vamos calcular a integral pelos caminhos

,

,temos que:
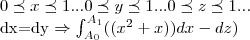
![\int_{0}^{1}({x}^{2}+x)dx-\int_{0}^{1}dz=(({x}^
{3}/3)+({x}^{2}/2)[0,1]-z[0,1]=(1/3)+(1/2)-1=-1/6... \int_{0}^{1}({x}^{2}+x)dx-\int_{0}^{1}dz=(({x}^
{3}/3)+({x}^{2}/2)[0,1]-z[0,1]=(1/3)+(1/2)-1=-1/6...](/latexrender/pictures/6aca2edd13854094e0c12aa3c83bc5a1.png)
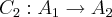
,temos:

sentido negativo,logo:
![\int_{{A}_{1}}^{{A}_{2}}(-dz)=[tex]\int_{0}^{1}-dz=\int_{1}^{0}dz=z[1,0]=1... \int_{{A}_{1}}^{{A}_{2}}(-dz)=[tex]\int_{0}^{1}-dz=\int_{1}^{0}dz=z[1,0]=1...](/latexrender/pictures/84ecced62382ad3ceea5983a79cbf3de.png)
...logo o valor da integral sera a soma dos caminhos

,ou seja:

se tomarmos o caminho
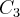
,ou seja
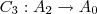
,teriamos o valor da integral igual a zero,ou seja:
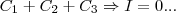
,fechariamos a linha poligonal...
de fato:
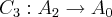
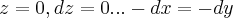
,tanto x,y variara negativamente:
![\int_{{A}_{2}}^{{A}_{0}}-({x}^{2}+x)dx=-(({x}^{3}/3)+({x}^{2}/2)[(1,1,0),(0,0,0)]=-((1/3)+(1/2)=-5/6... \int_{{A}_{2}}^{{A}_{0}}-({x}^{2}+x)dx=-(({x}^{3}/3)+({x}^{2}/2)[(1,1,0),(0,0,0)]=-((1/3)+(1/2)=-5/6...](/latexrender/pictures/01a69c1f06307e32f654149c7cd4a6fa.png)

-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por pedro22132938 » Seg Jan 02, 2017 00:29
por pedro22132938 » Seg Jan 02, 2017 00:29
Então, minha resposta está correta? De fato é 0 o resultado, pois tenho que fechar a poligonal não?
-
pedro22132938
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Mar 22, 2015 17:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: EAD
- Andamento: formado
 por adauto martins » Seg Jan 02, 2017 15:14
por adauto martins » Seg Jan 02, 2017 15:14
meu caro pedro,
sua resposta esta incorreta,pois vc usando o metodo de parametrizaçao deva ter fechado a poligonal...
a integral de linha mede a area abaixo da curva(caminho,linha,interseçao de superficies e etc...) em relaçao a um dos planos X0Y,X0Z,Y0Z...é como na integral de uma variavel,
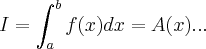
...metodo da poligonal fechado tem seu uso no calculo de integraçao de variaveis compelexas,calculo do numero de residuos em um compacto qquer...entao é isso...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- dúvida de cálculo 3 - integral de linha
por peridotito » Sex Nov 20, 2020 22:26
- 0 Respostas
- 5848 Exibições
- Última mensagem por peridotito

Sex Nov 20, 2020 22:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral de linha - 2
por DanielFerreira » Dom Jun 03, 2012 16:14
- 2 Respostas
- 2968 Exibições
- Última mensagem por DanielFerreira

Dom Jun 03, 2012 19:14
Cálculo: Limites, Derivadas e Integrais
-
- Integral de linha
por calc3 » Dom Jun 07, 2015 11:43
- 0 Respostas
- 3224 Exibições
- Última mensagem por calc3

Dom Jun 07, 2015 11:43
Cálculo: Limites, Derivadas e Integrais
-
- Integral de linha - Trabalho
 por Bruhh » Ter Jul 05, 2011 16:55
por Bruhh » Ter Jul 05, 2011 16:55
- 1 Respostas
- 3320 Exibições
- Última mensagem por LuizAquino

Ter Jul 05, 2011 19:10
Cálculo: Limites, Derivadas e Integrais
-
- [Integral de Linha] Teoria
por Claudin » Qui Jul 25, 2013 23:47
- 0 Respostas
- 2096 Exibições
- Última mensagem por Claudin

Qui Jul 25, 2013 23:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
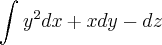 e
e  é a poligonal de vértices A0 = (0,0,0), A1=(1,1,1) e A2=(1,1,0), orientada de A0 para A2.
é a poligonal de vértices A0 = (0,0,0), A1=(1,1,1) e A2=(1,1,0), orientada de A0 para A2.

 ,
, ,temos que:
,temos que: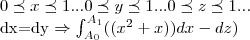
![\int_{0}^{1}({x}^{2}+x)dx-\int_{0}^{1}dz=(({x}^
{3}/3)+({x}^{2}/2)[0,1]-z[0,1]=(1/3)+(1/2)-1=-1/6... \int_{0}^{1}({x}^{2}+x)dx-\int_{0}^{1}dz=(({x}^
{3}/3)+({x}^{2}/2)[0,1]-z[0,1]=(1/3)+(1/2)-1=-1/6...](/latexrender/pictures/6aca2edd13854094e0c12aa3c83bc5a1.png)
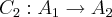 ,temos:
,temos: sentido negativo,logo:
sentido negativo,logo:![\int_{{A}_{1}}^{{A}_{2}}(-dz)=[tex]\int_{0}^{1}-dz=\int_{1}^{0}dz=z[1,0]=1... \int_{{A}_{1}}^{{A}_{2}}(-dz)=[tex]\int_{0}^{1}-dz=\int_{1}^{0}dz=z[1,0]=1...](/latexrender/pictures/84ecced62382ad3ceea5983a79cbf3de.png) ...logo o valor da integral sera a soma dos caminhos
...logo o valor da integral sera a soma dos caminhos ,ou seja:
,ou seja:
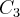 ,ou seja
,ou seja 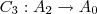 ,teriamos o valor da integral igual a zero,ou seja:
,teriamos o valor da integral igual a zero,ou seja: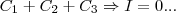 ,fechariamos a linha poligonal...
,fechariamos a linha poligonal...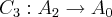
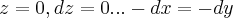 ,tanto x,y variara negativamente:
,tanto x,y variara negativamente:![\int_{{A}_{2}}^{{A}_{0}}-({x}^{2}+x)dx=-(({x}^{3}/3)+({x}^{2}/2)[(1,1,0),(0,0,0)]=-((1/3)+(1/2)=-5/6... \int_{{A}_{2}}^{{A}_{0}}-({x}^{2}+x)dx=-(({x}^{3}/3)+({x}^{2}/2)[(1,1,0),(0,0,0)]=-((1/3)+(1/2)=-5/6...](/latexrender/pictures/01a69c1f06307e32f654149c7cd4a6fa.png)


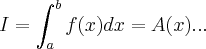 ...metodo da poligonal fechado tem seu uso no calculo de integraçao de variaveis compelexas,calculo do numero de residuos em um compacto qquer...entao é isso...
...metodo da poligonal fechado tem seu uso no calculo de integraçao de variaveis compelexas,calculo do numero de residuos em um compacto qquer...entao é isso...![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.