 por CaAtr » Ter Mar 09, 2010 20:23
por CaAtr » Ter Mar 09, 2010 20:23
UFMG - O valor da expressão
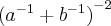
é:
Simplifique a expressão A =
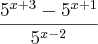
Tentei de formas possiveis e imaginaveis e nao cheguei a resultado nenhum! Quem puder me ajudar, Obrigada desde ja!

-
CaAtr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mar 09, 2010 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Ter Mar 09, 2010 22:04
por Cleyson007 » Ter Mar 09, 2010 22:04
Boa noite CaAtr!
Seja bem vindo (a) ao Ajuda Matemática!

Vai uma ajuda no primeiro exercício:

Uma incógnita (ou um número) elevado a expoente -1, significa seu inverso, veja:
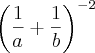
Tirando o m.m.c, temos:

Resolvendo agora o expoente -2:

Desenvolvendo o denominador:

Quanto a sua segunda dúvida, acho que o estudo dos exponenciais pode ajudar em algo. Comente qualquer dúvida

Espero ter ajudado

Até mais.
Editado pela última vez por
Cleyson007 em Ter Mar 09, 2010 22:32, em um total de 1 vez.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Ter Mar 09, 2010 22:12
por Molina » Ter Mar 09, 2010 22:12
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por CaAtr » Ter Mar 09, 2010 22:17
por CaAtr » Ter Mar 09, 2010 22:17
Nossa nem acredito que era so isso, bati tanto a cabeça e nao consegui!! Obrigada pela dica da segunda questão, se eu tiver duvidas te comunicarei!! Obrigada
-
CaAtr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mar 09, 2010 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2279 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1727 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- POTENCIAÇÃO
por DANIELA » Sex Set 25, 2009 16:48
- 5 Respostas
- 3714 Exibições
- Última mensagem por DanielFerreira

Seg Set 28, 2009 10:20
Álgebra Elementar
-
- potenciação
por leandrofelip » Ter Fev 23, 2010 00:10
- 1 Respostas
- 2007 Exibições
- Última mensagem por Marcampucio

Ter Fev 23, 2010 12:56
Sistemas de Equações
-
- Potenciação
por Juliane » Ter Jan 11, 2011 16:43
- 2 Respostas
- 1700 Exibições
- Última mensagem por meuemail

Ter Jan 11, 2011 22:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
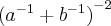 é:
é: 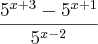


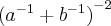 é:
é: 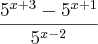




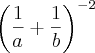






é:
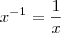
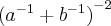

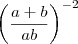
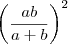
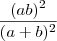

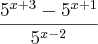
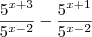








 , avisa que eu resolvo.
, avisa que eu resolvo.

