 por Saulosilva » Seg Out 27, 2014 16:39
por Saulosilva » Seg Out 27, 2014 16:39
Estou com uma dúvida quanto a derivação da equação que representa o Volume na questão seguinte, e se possível postarem um gabarito para eu corrigir com a minha, ficaria grato.
Drenagem de um reservatório hemisférico. Água escoa a uma taxa de 6m^3/min de um reservatório hemisférico com raio de 13m, mostrado aqui em perfil. Responda as questões a seguir, sendo o volume da água em um recipiente hemisférico de raio r dado por (não vou usar o Latex por falta de treino e tempo no momento !) V=(pi/3).y².(3R-y), quando a água tiver y metros de profundidade.
pois bem, a letra é pede a taxa de variação quando a profundidade for 8 metros, e pare isso fui derivar a fórmula de Volume, mas não consegui (acho que não!) e por isso peço a ajuda de vocês, obrigado !
-
Saulosilva
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 27, 2014 15:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Saulosilva » Ter Out 28, 2014 08:53
por Saulosilva » Ter Out 28, 2014 08:53
Bem, agora gostaria só mesmo de uma resolução da derivada de volume (isolando y' ) pra conferir com a minha resposta.. obrigado
-
Saulosilva
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 27, 2014 15:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por adauto martins » Qua Out 29, 2014 15:27
por adauto martins » Qua Out 29, 2014 15:27
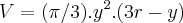
...dV/dt=
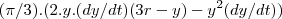
...
dV/dt(taxa de variaçao cubica),dy/dt(taxa de variaçao linear)...agora e usar os dados e calcular...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por leandrocalixto » Ter Out 04, 2016 15:19
por leandrocalixto » Ter Out 04, 2016 15:19
Olá, você tem como mandar os cálculos dessa questão aí?
-
leandrocalixto
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Out 04, 2016 15:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Construção civil
- Andamento: cursando
 por adauto martins » Qua Out 05, 2016 11:55
por adauto martins » Qua Out 05, 2016 11:55
dados do problema:
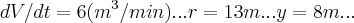
...
o que se pede:
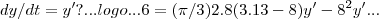
...termine o CALCULO!,ou seja faça as contas...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxa de variação
por felipe_ad » Ter Jun 29, 2010 19:44
- 2 Respostas
- 60614 Exibições
- Última mensagem por Guill

Ter Fev 21, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variação
 por AlbertoAM » Sáb Mai 21, 2011 14:23
por AlbertoAM » Sáb Mai 21, 2011 14:23
- 1 Respostas
- 5495 Exibições
- Última mensagem por LuizAquino

Dom Mai 22, 2011 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por AlbertoAM » Sáb Mai 28, 2011 15:53
por AlbertoAM » Sáb Mai 28, 2011 15:53
- 10 Respostas
- 10641 Exibições
- Última mensagem por AlbertoAM

Ter Mai 31, 2011 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por Pollyanna Moraes » Sáb Out 22, 2011 17:37
por Pollyanna Moraes » Sáb Out 22, 2011 17:37
- 1 Respostas
- 8463 Exibições
- Última mensagem por LuizAquino

Dom Out 23, 2011 10:15
Cálculo: Limites, Derivadas e Integrais
-
- taxa de variacao
por cal12 » Dom Nov 27, 2011 16:46
- 3 Respostas
- 5405 Exibições
- Última mensagem por Russman

Sex Jun 29, 2012 22:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


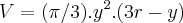 ...dV/dt=
...dV/dt=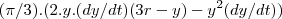 ...
...
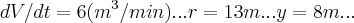 ...
...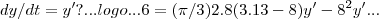 ...termine o CALCULO!,ou seja faça as contas...
...termine o CALCULO!,ou seja faça as contas...
 .
.
 :
: