 por Rike Morais » Sex Jul 08, 2016 16:41
por Rike Morais » Sex Jul 08, 2016 16:41
Boa tarde galera!
Estou com uma dúvida simples. Tenho as seguintes funções:
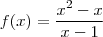

Eu preciso descobrir se

, então comecei:
![f(x)=\frac{x^2-x}{x-1}[/b] = [b]\frac{x^2-x^1}{x-1} = \frac{x}{x-1} f(x)=\frac{x^2-x}{x-1}[/b] = [b]\frac{x^2-x^1}{x-1} = \frac{x}{x-1}](/latexrender/pictures/09afe009b3d45cb603145bac9e1d16bd.png)
E é aqui que me deparo com o problema: Eu não posso eliminar os x. A conta acaba aí?
Muito Obrigado pela ajuda!
Henrique Morais
Consultor de TI
Graduando em Estatística (UFS)
-
Rike Morais
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jan 14, 2012 16:57
- Localização: Aracaju - Se
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
-
 por Daniel Bosi » Sex Jul 08, 2016 17:15
por Daniel Bosi » Sex Jul 08, 2016 17:15
Olá, Rike. Tente começar igualando as duas funções:

A partir disso basta multiplicar ambos os lados por

:
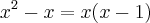
Aplicando a distributiva no lado direito da igualdade vemos que, de fato, as funções são iguais:

-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Rike Morais » Sex Jul 08, 2016 17:22
por Rike Morais » Sex Jul 08, 2016 17:22
Muito bom! Obrigado Daniel!


Henrique Morais
Consultor de TI
Graduando em Estatística (UFS)
-
Rike Morais
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jan 14, 2012 16:57
- Localização: Aracaju - Se
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
-
 por Daniel Bosi » Sex Jul 08, 2016 17:44
por Daniel Bosi » Sex Jul 08, 2016 17:44
Só perceba um detalhe, Rike:
A função

não está definida para

(pois caso x seja 1, o denominador dá zero e teremos uma divisão por zero). Portanto, não podemos dizer que as funções são iguais (pois não existe uma correspondência para o ponto

na imagem), embora seja possível mostrar algebricamente que as expressões são equivalentes para valores de x diferentes de 1.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função simples (UFF-RJ)
por guijermous » Ter Fev 16, 2010 12:08
- 2 Respostas
- 1907 Exibições
- Última mensagem por guijermous

Ter Fev 16, 2010 12:40
Funções
-
- Função simples
por Pad » Ter Jul 10, 2012 20:30
- 1 Respostas
- 3850 Exibições
- Última mensagem por Russman

Ter Jul 10, 2012 21:39
Funções
-
- Função simples
por Striker694 » Qui Jun 30, 2016 23:30
- 1 Respostas
- 3982 Exibições
- Última mensagem por adauto martins

Qui Jul 07, 2016 11:49
Funções
-
- Função simples
por esdraslima » Sáb Jul 09, 2016 02:00
- 1 Respostas
- 2210 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 09, 2016 12:32
Funções
-
- função simples de derivada
por miumatos » Dom Mar 18, 2012 13:06
- 2 Respostas
- 2263 Exibições
- Última mensagem por miumatos

Dom Mar 18, 2012 15:29
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
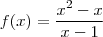

 , então comecei:
, então comecei:![f(x)=\frac{x^2-x}{x-1}[/b] = [b]\frac{x^2-x^1}{x-1} = \frac{x}{x-1} f(x)=\frac{x^2-x}{x-1}[/b] = [b]\frac{x^2-x^1}{x-1} = \frac{x}{x-1}](/latexrender/pictures/09afe009b3d45cb603145bac9e1d16bd.png)

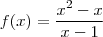

 , então comecei:
, então comecei:![f(x)=\frac{x^2-x}{x-1}[/b] = [b]\frac{x^2-x^1}{x-1} = \frac{x}{x-1} f(x)=\frac{x^2-x}{x-1}[/b] = [b]\frac{x^2-x^1}{x-1} = \frac{x}{x-1}](/latexrender/pictures/09afe009b3d45cb603145bac9e1d16bd.png)


 :
: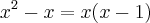





 não está definida para
não está definida para  (pois caso x seja 1, o denominador dá zero e teremos uma divisão por zero). Portanto, não podemos dizer que as funções são iguais (pois não existe uma correspondência para o ponto
(pois caso x seja 1, o denominador dá zero e teremos uma divisão por zero). Portanto, não podemos dizer que as funções são iguais (pois não existe uma correspondência para o ponto  na imagem), embora seja possível mostrar algebricamente que as expressões são equivalentes para valores de x diferentes de 1.
na imagem), embora seja possível mostrar algebricamente que as expressões são equivalentes para valores de x diferentes de 1.

 .
.
 :
: