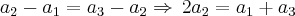por zenildo » Qui Mai 12, 2016 23:04
Essa questão 29 da FUVEST não consegui fazer por conta de não entendê-la em relação a incógnita que ela tem. Poderia fazer de forma detalhada para que eu pudesse entender, pois esse tópico de trigonometria ainda falta alguns exercícios para esta afiado.
- Anexos
-
-
zenildo
- Colaborador Voluntário
-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
por zenildo » Dom Mai 15, 2016 21:39
Olá Cleyson, eu não compreendi como surgiu essas raízes. Pode demonstrar como vc extraiu do círculo trigonométrico para fazer desse modo? Eu, infelizmente,não compreendi a sua linha de raciocínio.
-
zenildo
- Colaborador Voluntário
-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
por Cleyson007 » Qua Mai 18, 2016 16:08
Olá!
Repare que pi/12 = 15° (pois pi rad = 180°). Logo, temos a1= sen (15°) = sen (45° - 30°).
sen (a - b) = sen (a) * cos (b) - sen (b) * cos (a).
Repare que a = 45° e b = 30°.
Consegue concluir sozinho?
Att,
Prof° Cleyson
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Oi,Mestre...
por Fiel8 » Qua Jul 01, 2009 17:07
- 0 Respostas
- 1019 Exibições
- Última mensagem por Fiel8
Qua Jul 01, 2009 17:07
Sistemas de Equações
-
- Hello...mestre...
por Fiel8 » Qua Jul 01, 2009 17:23
- 1 Respostas
- 1456 Exibições
- Última mensagem por Cleyson007
Seg Jul 06, 2009 17:57
Sistemas de Equações
-
- E ai mestre..
por Fiel8 » Qua Jul 01, 2009 17:43
- 1 Respostas
- 1185 Exibições
- Última mensagem por Neperiano
Sáb Set 17, 2011 21:34
Funções
-
- [porcentagem] Auxilio na solução do problema
por rafynhasantos » Sáb Jun 21, 2008 22:58
- 1 Respostas
- 1530 Exibições
- Última mensagem por Molina
Sáb Jun 21, 2008 23:29
Álgebra Elementar
-
- [cálculo exponencial] auxilio em resolução
por zaspers » Ter Out 08, 2013 07:02
- 2 Respostas
- 1398 Exibições
- Última mensagem por zaspers
Sáb Out 12, 2013 10:26
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
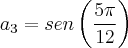
![{a}_{1}=\left(\frac{\sqrt[]{6}-\sqrt[]{2}}{4} \right)](/latexrender/pictures/99e22ce525f22a2ab12bdbad787d4386.png "{a}_{1}=\left(\frac{\sqrt[]{6}-\sqrt[]{2}}{4} \right)")
![{a}_{3}=sen\left(\frac{5\pi}{12} \right)=\left(\frac{\sqrt[]{6}+\sqrt[]{2}}{4} \right)](/latexrender/pictures/b29734d0e353da38a2cb21ae71e454ac.png "{a}_{3}=sen\left(\frac{5\pi}{12} \right)=\left(\frac{\sqrt[]{6}+\sqrt[]{2}}{4} \right)")
