 por zenildo » Seg Mai 09, 2016 01:49
por zenildo » Seg Mai 09, 2016 01:49
A soma do cos^2 0°+ cos^2 2°+ cos^2 4°+cos^2 4°+ cos^2 6°+....+cos^2 358°+ cos^2 360°, é igual a:
A) 316 obs: olá, todas as minhas tentativas até agora de resolver
B) 270 este problema foram frustrantes, a medida que, não
C) 181 não encontrei a resposta certa.
D) 180
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por nakagumahissao » Seg Mai 09, 2016 07:18
por nakagumahissao » Seg Mai 09, 2016 07:18
cos^2 0°+ cos^2 2°+ cos^2 4°+cos^2 4°
Repetido duas vezes o 4. É isso mesmo?
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por zenildo » Seg Mai 09, 2016 11:22
por zenildo » Seg Mai 09, 2016 11:22
Sim é isto mesmo Nakagumassuma.Estava escrito assim no problema.
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por nakagumahissao » Qui Mai 12, 2016 03:03
por nakagumahissao » Qui Mai 12, 2016 03:03
A questão parece ter sido colocada de forma diferente. De qualquer forma para agilizar e não ter que resolver a questao novamente:
https://br.answers.yahoo.com/question/i ... 000AA6JkTJpossui a soma ateh 360 sem repetir o 4.
Portanto, a resposta do link acima estah correta pois 1/3 do tempo os números ficam próximos de 1 enquanto que os outros 1/3 dos valores se situam proximos de 0.5 e outros 1/3 proximos de 0. Assim, de 0 graus ateh 90, temos uma PA de razao 2 onde o primeiro termo eh 0 e o ultimo termo eh 90, ou seja
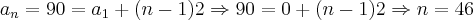
Sao 46 termos. O que equivale a dizer que 46/3 = 15 aproximadamente ficam em torno de 1 e outros 15 em torno de 1/2, ou seja, 15 + 15/2 = 23 aproximadamente
Se repetirmos isso para os quatro quadrantes, e considerando que os cossenos estão elevados ao quadrado, ou seja, sempre positivos, temos então que multiplicar esse valor por 4, ou seja, 23 x 4 = 92 aproximadamente.
Fiz um aplicativo para verificar isso em valores e mostra-los para voce e os resultados sao:

Se desejar baixar o aplicativo:
https://drive.google.com/file/d/0B05xwwRHqMfYelNBaXpacFR0TDA/view?usp=sharingAgora, no seu caso, basta adicionar ao resultado mais um Cos^2(4), o que daria 92 + 0.9951340344 =92.99513403
Nao mudaria muito o resultado. Basta agora escolher a opcao cujo valor seja mais proximo de 92.99513403
Veja que o valor final correto da soma seria: 90.6024899481915 + cos^2(4) = 91.59762398
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por zenildo » Qui Mai 12, 2016 22:43
por zenildo » Qui Mai 12, 2016 22:43
Como faço pra saber muita matemática como vc? Parabéns, bem feita a questão!
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda aqui com essa questão de função
por Ronaldobb » Qui Set 20, 2012 19:41
- 7 Respostas
- 3353 Exibições
- Última mensagem por Ronaldobb

Qui Set 20, 2012 22:34
Funções
-
- Lógica e Conjuntos, questão cabulosa.
por legendandom » Qui Abr 15, 2010 15:50
- 1 Respostas
- 2709 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 19:58
Álgebra Elementar
-
- Ajuda aqui!
por Liahtz » Sex Ago 07, 2015 17:38
- 1 Respostas
- 10897 Exibições
- Última mensagem por nakagumahissao

Sáb Ago 08, 2015 11:33
Matrizes e Determinantes
-
- ajuda aqui!
 por zenildo » Seg Mai 09, 2016 01:18
por zenildo » Seg Mai 09, 2016 01:18
- 5 Respostas
- 10408 Exibições
- Última mensagem por zenildo

Qui Mai 12, 2016 22:41
Trigonometria
-
- ajuda aqui por favor
 por zenildo » Qui Mai 12, 2016 23:55
por zenildo » Qui Mai 12, 2016 23:55
- 0 Respostas
- 2659 Exibições
- Última mensagem por zenildo

Qui Mai 12, 2016 23:55
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


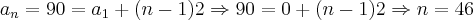



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.