Boa tarde!
Domínio da função:

Derivando:

Para obter os pontos críticos devemos encontrar os valores onde a derivada não existe ou valha zero. Portanto:
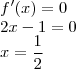
Este ponto não pertence ao domínio.
Não há derivada em x=0 e em x=1, mas também não pertencem ao domínio.
Analisando o sinal da derivada primeira:
2x-1 ==> x=1/2 ==> x<1/2 (negativa) x>1/2 (positiva)
x ==> x=0 ==> x<0 (negativa) x>0 (positiva)
x-1 ==> x=1 ==> x<1 (negativa) x>1 (positiva)
- Código: Selecionar todos
2x-1------(-)----------------(-)------(1/2)-------(+)-----------------(+)-------
x----------(-)------(0)------(+)-------------------(+)-----------------(+)-------
x-1--------(-)---------------(-)--------------------(-)------(1)-------(+)--------
f'(x)-------(-)-----(0)-------(+)------(1/2)-------(-)------(1)-------(+)--------
f'(x)=(2x-1)/((x(x-1))
Então, para valores menores do que 0 a derivada é negativa, portanto, função DECRESCENTE.
Para valores maiores do que 1 a derivada é positiva, portanto, função CRESCENTE.
a) Não há pontos de mínimo local.
b) Não há pontos de máximo local.
c) f(x) é crescente para x>1
d) f(x) é decrescente para x<0
Espero ter ajudado!





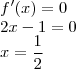



 .
.



