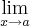 (x^k - a^k ) = 0
(x^k - a^k ) = 0

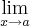 (x^k - a^k ) = 0
(x^k - a^k ) = 0
 é fácil verificar o resultado . No caso geral , em que k é um natural qualquer
é fácil verificar o resultado . No caso geral , em que k é um natural qualquer 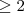 ,fatore x^k - a^k ( divida o polinômio x^k - a^k por x-a ) . Feito isto , vamos poder escrever x^k - a^k como (x-a) q(x) , onde q(x) é um polinômio de grau k-1 . Em seguida ,note o seguinte , ao trabalharmos com x próximo de a , podemos majorar |x| (e.g . por 1 + |a| ) , e consequentemente teremos |q(x)| < M (p algum M > 0 ) . Dai vem :
,fatore x^k - a^k ( divida o polinômio x^k - a^k por x-a ) . Feito isto , vamos poder escrever x^k - a^k como (x-a) q(x) , onde q(x) é um polinômio de grau k-1 . Em seguida ,note o seguinte , ao trabalharmos com x próximo de a , podemos majorar |x| (e.g . por 1 + |a| ) , e consequentemente teremos |q(x)| < M (p algum M > 0 ) . Dai vem : 
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.



