1) Para que a parábola
 NÃO intercepte a reta y = 3 , devemos ter quais valores de M ? ( tenho mínima idéia)
NÃO intercepte a reta y = 3 , devemos ter quais valores de M ? ( tenho mínima idéia)2) Os pontos (0,0) e (2,1) estão no gráfico de uma função quadrática F. O mínimo de F é assumido no ponto de abcissa
 . Logo, o valor de F(1) é?
. Logo, o valor de F(1) é?3) O valor em reais de uma pedra semipreciosa é sempre numericamente igual ao quadrado de sua massa, em gramas. Infelizmente uma dessa pedras, de 8 gramas, caiu e se partiu em dois pedaços. O prejuízo foi o maior possível. Em relação ao valor original , o prejuízo foi de? ( não sei como calcular o maior possível)
4) O conjunto solução de
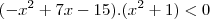 é? (deu resultado diferente)
é? (deu resultado diferente)Todos esses são da Fuvest e não consegui faze-los. Se poderem me ajudar, dar dicas, qualquer ajuda estou grato
Obrigado



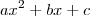 . Se o ponto
. Se o ponto 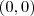 pertence a essa função, então:
pertence a essa função, então:
 .
.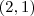 também pertence a essa função:
também pertence a essa função: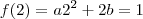
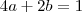
 . Como o valor mínimo é a média aritmética das raízes, e uma delas é zero:
. Como o valor mínimo é a média aritmética das raízes, e uma delas é zero: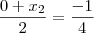
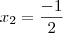
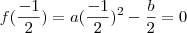
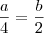
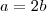
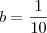 e
e 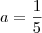 . A função então é:
. A função então é: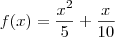
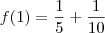
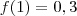 .
.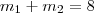 , porque a soma das massas permanece constante mesmo depois de quebrar. O enunciado diz que o preço é:
, porque a soma das massas permanece constante mesmo depois de quebrar. O enunciado diz que o preço é: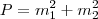
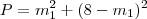
 ), então prejuízo foi de 50%.
), então prejuízo foi de 50%. a zero, estamos tentando encontrar intersecções com o eixo das abscissas, certo? Tente igualar
a zero, estamos tentando encontrar intersecções com o eixo das abscissas, certo? Tente igualar  e resolver de maneira que delta dê menor que zero.
e resolver de maneira que delta dê menor que zero.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.