 por davifd_ » Ter Ago 18, 2015 15:56
por davifd_ » Ter Ago 18, 2015 15:56
Não aprendi a usar ainda o editor de fórmulas por isso anexei o limite. Minha dúvida é como calcular limites infinitos envolvendo séries, agradeço antecipadamente
- Anexos
-
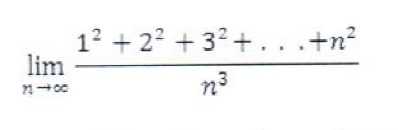
- Limite
- limite.jpg (8.28 KiB) Exibido 10641 vezes
-
davifd_
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Ago 18, 2015 15:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: formado
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por davifd_ » Ter Ago 18, 2015 23:40
por davifd_ » Ter Ago 18, 2015 23:40
nakagumahissao
inicialmente eu pensei assim tb, porém a resposta desse limite é 1/3, tem que fazer alguma jogada com o limite da série
-
davifd_
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Ago 18, 2015 15:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: formado
 por nakagumahissao » Ter Ago 18, 2015 23:54
por nakagumahissao » Ter Ago 18, 2015 23:54
davifd_,
Então, como esse limite possui uma indefinição na fração, tentei por L'Hôpital também, mas o resultado é o mesmo! Apliquei duas vezes:


Vou pensar mais um pouco e entro em contato em breve. Por um acaso, poderia me informar de onde tirou esse problema (livro, autor, página, volume, edição?) por favor?
Grato
Sandro
Editado pela última vez por
nakagumahissao em Qua Ago 19, 2015 01:53, em um total de 1 vez.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por davifd_ » Ter Ago 18, 2015 23:56
por davifd_ » Ter Ago 18, 2015 23:56
[quote="nakagumahissao"]
Esse problema foi de um concurso para fuzileiro naval, área de máquinas, é de engenharia ano 2014
-
davifd_
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Ago 18, 2015 15:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: formado
 por nakagumahissao » Qua Ago 19, 2015 00:27
por nakagumahissao » Qua Ago 19, 2015 00:27
davifd_,
Então davifd, coloquei esta sua questão no Mapple que é um software voltado para a matemática e cálculos científicos e o resultado foi esse que calculamos mesmo, ou seja, zero. Acredito que o gabarito esteja errado.
https://goo.gl/photos/iGei8WW8WsQ9ZLQu9
Acho que agora só aguardando outro professor passar por aqui para ajudar a sanar esta dúvida. Mas como já estou respondendo, acredito que outro professor não olhará este thread. Talvez se você postar novamente o problema para ter uma segunda opinião, quem sabe?
Grato
Sandro
Editado pela última vez por
nakagumahissao em Qua Ago 19, 2015 01:53, em um total de 1 vez.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por davifd_ » Qua Ago 19, 2015 00:57
por davifd_ » Qua Ago 19, 2015 00:57
[quote="nakagumahissao"]davifd_,
Opa, eu joguei no mathcad e deu 1/3, vc definiu errado a série eu acho... Tem que por x^2 e indo de x=1 até n o somatório
-
davifd_
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Ago 18, 2015 15:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: formado
 por nakagumahissao » Qua Ago 19, 2015 00:58
por nakagumahissao » Qua Ago 19, 2015 00:58
Vou tentar aqui. Já retorno.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por nakagumahissao » Qua Ago 19, 2015 01:27
por nakagumahissao » Qua Ago 19, 2015 01:27
Realmente:
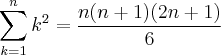
Utilizando esta identidade teremos:
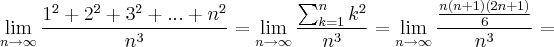
![= \lim_{n \rightarrow \infty} \frac{n(n+1)(2n+1)}{6n^3} = \lim_{n \rightarrow \infty} \frac{(n+1)(2n+1)}{6n^2}\;\;\; [1] = \lim_{n \rightarrow \infty} \frac{n(n+1)(2n+1)}{6n^3} = \lim_{n \rightarrow \infty} \frac{(n+1)(2n+1)}{6n^2}\;\;\; [1]](/latexrender/pictures/24d3c6894bf152b9c27e6c2e10e885e7.png)
Usando L'Hôpital duas vezes, tem-se:
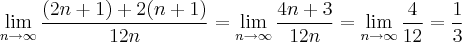
Nossa! Essa foi difícil! heheheh - Acho que agora está certo! Desculpe pelo erro! Afinal, não somos infalíveis!
Para o caso de desejar saber:
http://www.9math.com/book/sum-squares-f ... al-numbersEu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por davifd_ » Qua Ago 19, 2015 07:12
por davifd_ » Qua Ago 19, 2015 07:12
nakagumahissao
Obrigado! Com a identidade saiu fácil, o problema é decorar pra prova ne? hahahah
-
davifd_
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Ago 18, 2015 15:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: formado
 por nakagumahissao » Qua Ago 19, 2015 09:17
por nakagumahissao » Qua Ago 19, 2015 09:17
Verdade! Bons estudos
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] calculo de limite envolvendo n e x
por Henrique Bueno » Dom Abr 15, 2012 14:31
- 2 Respostas
- 2464 Exibições
- Última mensagem por Henrique Bueno

Seg Abr 16, 2012 19:08
Cálculo: Limites, Derivadas e Integrais
-
- limites infinitos
por oleve » Qua Jan 21, 2009 18:15
- 1 Respostas
- 3024 Exibições
- Última mensagem por Sandra Piedade

Sáb Jan 24, 2009 22:30
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos
por Sobreira » Sáb Out 13, 2012 00:07
- 7 Respostas
- 4517 Exibições
- Última mensagem por MarceloFantini

Ter Out 30, 2012 09:07
Cálculo: Limites, Derivadas e Integrais
-
- Limites Infinitos. Ajuda
por valeuleo » Qua Jun 22, 2011 12:39
- 4 Respostas
- 3132 Exibições
- Última mensagem por renatav

Dom Jun 26, 2011 22:46
Cálculo: Limites, Derivadas e Integrais
-
- Limites infinitos com modulo.
 por Sobreira » Sex Out 12, 2012 18:04
por Sobreira » Sex Out 12, 2012 18:04
- 13 Respostas
- 9038 Exibições
- Última mensagem por Sobreira

Sex Out 12, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



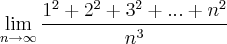

 . Assim, no numerador, todos os valores com exceção do último tenderão para zero quando n tender para o infinito. O último tenderá para 1 ficando da seguinte forma:
. Assim, no numerador, todos os valores com exceção do último tenderão para zero quando n tender para o infinito. O último tenderá para 1 ficando da seguinte forma:











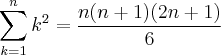
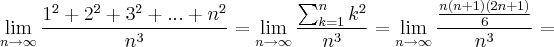
![= \lim_{n \rightarrow \infty} \frac{n(n+1)(2n+1)}{6n^3} = \lim_{n \rightarrow \infty} \frac{(n+1)(2n+1)}{6n^2}\;\;\; [1] = \lim_{n \rightarrow \infty} \frac{n(n+1)(2n+1)}{6n^3} = \lim_{n \rightarrow \infty} \frac{(n+1)(2n+1)}{6n^2}\;\;\; [1]](/latexrender/pictures/24d3c6894bf152b9c27e6c2e10e885e7.png)
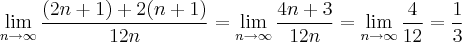





 , avisa que eu resolvo.
, avisa que eu resolvo.

