Ola, estou tentando resolver essa questao da ufsc que basicamente envolve apenas conceitos de potencia. Eu consigo anular o B e o C, mas nunca consigo cortar o A completamente, e como a resposta se trata de um numero puro, devo estar fazendo algo muito errado.
Resposta = 90.
OBS: Nao da pra ver direito na imagem, mas o C mais da esquerda é elevado a 8/3.
![\frac{120}{8}\left[2^8\cdot 4^{-3} \cdot \left(a^{4} \cdot b^{-2} \cdot c^{\frac{8}{3}} \right)^{3} \cdot 3^2 \cdot \left(\frac{b^3 \cdot a^{-4}}{a^{1} \cdot b^{0} \cdot c^{4} \right)^{2}} \right]^{\frac{1}{2}}](/latexrender/pictures/fd789da8558a850e046e0373af180617.png "\frac{120}{8}\left[2^8\cdot 4^{-3} \cdot \left(a^{4} \cdot b^{-2} \cdot c^{\frac{8}{3}} \right)^{3} \cdot 3^2 \cdot \left(\frac{b^3 \cdot a^{-4}}{a^{1} \cdot b^{0} \cdot c^{4} \right)^{2}} \right]^{\frac{1}{2}}")
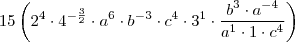
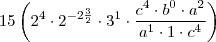
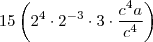
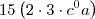
![\frac{120}{8}\left[2^8\cdot 4^{-3} \cdot a^{12} \cdot b^{-6} \cdot c^{8} \cdot 3^2 \cdot \frac{b^6 \cdot a^{-8}}{a^{2} \cdot b^{0} \cdot c^{8}} \right]^{\frac{1}{2}}](/latexrender/pictures/912ff80746c34896d51e40463af1cf31.png "\frac{120}{8}\left[2^8\cdot 4^{-3} \cdot a^{12} \cdot b^{-6} \cdot c^{8} \cdot 3^2 \cdot \frac{b^6 \cdot a^{-8}}{a^{2} \cdot b^{0} \cdot c^{8}} \right]^{\frac{1}{2}}")
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)