Solução:
![\sqrt{n+1}-\sqrt{n}=\frac{\left(\sqrt{n+1}\right)^2-\left(\sqrt{n}\right)^2}{\sqrt{n+1}+\sqrt{n}} \,\,\,\,\,\,\,\, [1] \sqrt{n+1}-\sqrt{n}=\frac{\left(\sqrt{n+1}\right)^2-\left(\sqrt{n}\right)^2}{\sqrt{n+1}+\sqrt{n}} \,\,\,\,\,\,\,\, [1]](/latexrender/pictures/b22b50402908816a6ef7d28ba69641ac.png)
No Passo acima, foi aplicado o seguinte:
Sejam dois números a e b, pertencentes aos reais, sendo que a - b diferente de zero. Então:
![a + b = (a+b) \frac{(a-b)}{(a-b)} = \frac{a^2 - b^2}{a - b} \,\,\,\,\,\,\,\,\,\,\, [2] a + b = (a+b) \frac{(a-b)}{(a-b)} = \frac{a^2 - b^2}{a - b} \,\,\,\,\,\,\,\,\,\,\, [2]](/latexrender/pictures/c0e09d552483662ad71d11ea121c9ba0.png)
Agora, considere que:

Substituindo estes valores acima em [2], obtem-se o resultado dado em [1] acima. Prosseguindo de [1] teremos:

Como n é sempre positivo, ignoramos o sinal do módulo acima. Desta maneira:
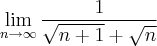
Veja que quando n tende ao infinito,
![n \rightarrow \infty \Rightarrow \frac{1}{\sqrt{\infty +1}+\sqrt{\infty}} \,\,\, e \,\,\, \frac{1}{\infty} \,\,\,\,\,\,\,\, [3] n \rightarrow \infty \Rightarrow \frac{1}{\sqrt{\infty +1}+\sqrt{\infty}} \,\,\, e \,\,\, \frac{1}{\infty} \,\,\,\,\,\,\,\, [3]](/latexrender/pictures/79a5cd992e6c026cf560a96c7f6f1131.png)
toda a fração tende para zero. Por isto, o resultado é zero.
Nota: As operações realizadas em [3] são apenas ilustrativas e não são válidas como operações. Na realidade, devemos pensar apenas no fato de que n está se aproximando do infinito, seja ele qual for. Infinito não é um número e portanto, não podemos fazer operações com ele. O que se quer dizer em [3] é que, quanto mais nós aumentamos o valor de n em direção ao infinito, teremos um n "grande" e que, estando no denominador da fração, faz com que 1 dividido por um número muito grande tem como resultado um número perto de zero e quanto mais aumentarmos o valor de "n", mais ainda nos aproximaremos de zero.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
![an = \sqrt[]{n+1} - \sqrt[]{n} an = \sqrt[]{n+1} - \sqrt[]{n}](/latexrender/pictures/aaf4e15ab7a29f5c0c19528913e74448.png)


![an = \sqrt[]{n+1} - \sqrt[]{n} an = \sqrt[]{n+1} - \sqrt[]{n}](/latexrender/pictures/aaf4e15ab7a29f5c0c19528913e74448.png)

![\sqrt{n+1}-\sqrt{n}=\frac{\left(\sqrt{n+1}\right)^2-\left(\sqrt{n}\right)^2}{\sqrt{n+1}+\sqrt{n}} \,\,\,\,\,\,\,\, [1] \sqrt{n+1}-\sqrt{n}=\frac{\left(\sqrt{n+1}\right)^2-\left(\sqrt{n}\right)^2}{\sqrt{n+1}+\sqrt{n}} \,\,\,\,\,\,\,\, [1]](/latexrender/pictures/b22b50402908816a6ef7d28ba69641ac.png)
![a + b = (a+b) \frac{(a-b)}{(a-b)} = \frac{a^2 - b^2}{a - b} \,\,\,\,\,\,\,\,\,\,\, [2] a + b = (a+b) \frac{(a-b)}{(a-b)} = \frac{a^2 - b^2}{a - b} \,\,\,\,\,\,\,\,\,\,\, [2]](/latexrender/pictures/c0e09d552483662ad71d11ea121c9ba0.png)


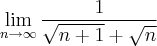
![n \rightarrow \infty \Rightarrow \frac{1}{\sqrt{\infty +1}+\sqrt{\infty}} \,\,\, e \,\,\, \frac{1}{\infty} \,\,\,\,\,\,\,\, [3] n \rightarrow \infty \Rightarrow \frac{1}{\sqrt{\infty +1}+\sqrt{\infty}} \,\,\, e \,\,\, \frac{1}{\infty} \,\,\,\,\,\,\,\, [3]](/latexrender/pictures/79a5cd992e6c026cf560a96c7f6f1131.png)




