 por Alane » Dom Ago 05, 2012 13:03
por Alane » Dom Ago 05, 2012 13:03
Francisco deve elaborar uma pesquisa com dois artrópodes distintos. Eles serão selecionados, ao acaso, da seguinte relação:aranha,besouro, barata, lagosta, camarão, formiga, ácaro, caranguejo, abelha, escorpião, carrapato e gafanhoto. Qual a probabilidade de que os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
Eu selecionei os artrópodes que não são insetos, deram 8. Então minha conclusão foi se temos 8 artrópodes não insetos que serão selecionados em pares então teremos 56 possibilidades, pois 8 x 7= 56
Então a possibilidade de escolha será 56/144. Simplificando ficou 7/18. Mas o resultado correto é o 7/22. Não consegui chegar a estes 22. Gostaria de saber como eu poderia estar chegando no resultado correto.
Obrigada ^^
-
Alane
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jul 05, 2012 22:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Dom Ago 05, 2012 15:34
por fraol » Dom Ago 05, 2012 15:34
Boa tarde,
Por favor, reveja a classificação, pois:
Insetos:besouro, barata, formiga, abelha, e gafanhoto
Não Insetos:aranha, lagosta, camarão, ácaro, caranguejo, escorpião e carrapato.
Qual a probabilidade de que os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
É a probabilidade do primeiro não ser inseto
e a probabilidade do segundo não ser inseto, i.e. :

.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por DanielFerreira » Dom Ago 05, 2012 15:48
por DanielFerreira » Dom Ago 05, 2012 15:48
Outra...
Combinações dos artrópodes: total
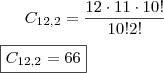 Combinações dos artrópodes
Combinações dos artrópodes: não são insetos
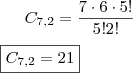
Segue que, a probabilidade procurada pode ser obtida calculando

Daí,

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por e8group » Dom Ago 05, 2012 15:50
por e8group » Dom Ago 05, 2012 15:50
Boa tarde .
Considere o espaço amostral
B = { aranha,besouro, barata, lagosta, camarão, formiga, ácaro, caranguejo, abelha, escorpião, carrapato , gafanhoto } ,
onde número de insetos equivale a 7 .
Logo a probabilidade de que ambos os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos é denotado por ,
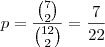
OBS.:
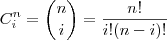
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Nina Luizet » Dom Ago 02, 2015 15:31
por Nina Luizet » Dom Ago 02, 2015 15:31
Olá, pessoal.
Percebi que vocês utilizaram a combinação chave com o método mais demorado.Aqui vai uma dica:
C12,2 = 12.11/2! = 66
C7,2 = 7.6/2! = 21
P = n(a)/n(e) = 21/66 = 7/22
Nina Luizet
-
Nina Luizet
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Fev 16, 2015 12:39
- Localização: Natal , RN , Brasil
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão CEFET-MG 2012
por Thulio_Parazi » Qui Abr 05, 2012 13:48
- 5 Respostas
- 4820 Exibições
- Última mensagem por fraol

Ter Abr 10, 2012 20:02
Trigonometria
-
- Cefet-mg 2012 questão 03
por Thulio_Parazi » Sex Abr 13, 2012 11:12
- 4 Respostas
- 4488 Exibições
- Última mensagem por fraol

Qua Abr 18, 2012 22:26
Logaritmos
-
- Questão UECE 2012
por Phaniemor » Qui Abr 18, 2013 11:33
- 1 Respostas
- 4479 Exibições
- Última mensagem por DanielFerreira

Qui Abr 18, 2013 12:01
Binômio de Newton
-
- Questão CEFET-MG graduação 2012
por Thulio_Parazi » Qui Abr 05, 2012 11:24
- 1 Respostas
- 2131 Exibições
- Última mensagem por fraol

Sex Abr 06, 2012 20:54
Trigonometria
-
- [PROBABILIDADE] Questão UNEB 2012
por yan_rulez » Qua Dez 12, 2012 00:23
- 5 Respostas
- 7583 Exibições
- Última mensagem por fraol

Qua Dez 12, 2012 20:32
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




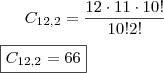
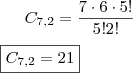



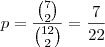
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
