Francisco deve elaborar uma pesquisa com dois artrópodes distintos. Eles serão selecionados, ao acaso, da seguinte relação:aranha,besouro, barata, lagosta, camarão, formiga, ácaro, caranguejo, abelha, escorpião, carrapato e gafanhoto. Qual a probabilidade de que os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
Eu selecionei os artrópodes que não são insetos, deram 8. Então minha conclusão foi se temos 8 artrópodes não insetos que serão selecionados em pares então teremos 56 possibilidades, pois 8 x 7= 56
Então a possibilidade de escolha será 56/144. Simplificando ficou 7/18. Mas o resultado correto é o 7/22. Não consegui chegar a estes 22. Gostaria de saber como eu poderia estar chegando no resultado correto.
Obrigada ^^




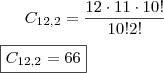
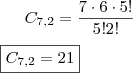



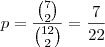
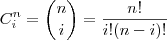

 .
.
 :
: