1) Seja A um conjunto de 11 elementos. O conjunto Y de todos os subconjuntos de A tem n elementos. Pode-se concluir que:
R: Estudando aqui no livro, vi essa fórmula: Se um conjunto tem n elementos então
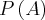 possui
possui  elementos
elementosEntão como A possui 11 elementos, fiz:
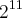 = n = 2.048
= n = 2.0482) Sendo A = {0, 1} e B = {2, 3}, o número de elementos [P(A) ? P(B)] é:
Nessa questão
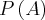 é achar o conjunto cujos elementos são todos os subconjuntos de A.
é achar o conjunto cujos elementos são todos os subconjuntos de A.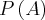 = {{
= {{ }, {0}, {1}, {0,1}}
}, {0}, {1}, {0,1}}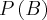 = {{
= {{ }, {2}, {3}, {2,3}}
}, {2}, {3}, {2,3}}Como pede [P(A) ? P(B)] = 1, cuja intersecção seria o {
 }
}Agora gostaria de uma ajuda pra responder essas questões abaixo, pois não tenho idéia nem de como começar.
3) O número de conjuntos X que satisfazem: {1, 2}
 X
X  {1, 2, 3, 4} é:
{1, 2, 3, 4} é:4) O número de elementos do conjunto A é
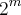 e o número de elementos do conjunto B é
e o número de elementos do conjunto B é  . O número de elementos de (A × B) é:
. O número de elementos de (A × B) é:5) Depois de N dias de férias, um estudante observa que:
I - Choveu 7 vezes, de manhã ou à tarde.
II - Quando chove de manhã, não chove à tarde.
III - Houve 5 tardes sem chuva.
IV - Houve 6 manhãs sem chuva.
O número N de dias de férias foi:




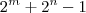


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
