Bom dia, gostaria de saber se consigo entrar com recurso nesta questão pois marquei C e no gabarito esta como A.
08 - Em um torneio de futebol amador, a cada rodada duas equipes se enfrentam. A equipe vitoriosa recebe 5 pontos e a perdedora não pontua; em caso de empate, cada uma das equipes recebe 3 pontos. Todos os pontos obtidos por uma equipe são somados, e aquele que tiver a maior pontuação no final do campeonato é declarado campeão. Sabendo que ao final do torneio a equipe dos Matemáticos obteve exatamente 37 pontos, considere as seguintes afirmativas: 1. A equipe dos Matemáticos jogou pelo menos 9 partidas nesse torneio. 2. A equipe dos Matemáticos obteve no máximo 6 empates. 3. A equipe dos Matemáticos foi derrotada pelo menos uma vez nesse torneio. Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente as afirmativas 1 e 2 são verdadeiras.
c) Somente as afirmativas 1 e 3 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras
Obrigado
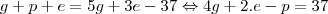
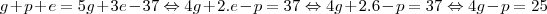
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.