 por Alvadorn » Sáb Fev 20, 2010 12:55
por Alvadorn » Sáb Fev 20, 2010 12:55

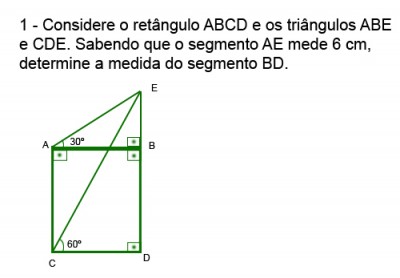
Gente eu to com uma pequena dificuldade na resolução dessa questão, eu não estou sabendo utilizar o dado fornecido pela mesma, em função do segmento requisitado, o BD
Alguém poderia me encaminhar como iniciar a solução da mesma?
Desde já agradeço a atenção!
-
Alvadorn
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Fev 20, 2010 12:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Rodrigo Tomaz » Sáb Fev 20, 2010 14:24
por Rodrigo Tomaz » Sáb Fev 20, 2010 14:24
Bom dia!
Estava dando uma olhadinha em sua questão e espero poder ajudá-lo.
No enunciado fornece apenas os ângulos e um lado.
Se você observar o angulo do vértice A é dividido em dois, um de 30° outro de 90°, formando um angulo de 120°.
O angulo do vértice C, também dividido em dois, mede ao todo 90°. Para saber quanto mede a parte restante subtrai-se com os 60º dados obtendo-se 30°.
Se formos olhar como resultou, teremos um triângulo ACE, com ângulos 120°,30 e 30°.
Como o triâgulo observado acima tem dois ângulos iguais, obrigatoriamente terá dois lados iguais (é um triângulo isósceles).
O lado fornecido AE, que mede 6cm, pertence ao triângulo e por não ser oposto ao ângulo diferente o lado AC terá o mesmo valor de 6cm.
Como o lado desejado pertence ao retângulo ABCD, e no mesmo AB=CD e AC=BD logo AC=BD=6cm
Essa questão também pode ser resolvida por outras linhas de raciocínio. Outra por exemplo seria fazer o jogo de senos, cossenos e tangentes descobrindo lado por lado até então chegar no valor desejado.
Eu acho que é isso,
Espero ter te ajudado
- Anexos
-
-
Rodrigo Tomaz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Fev 19, 2010 10:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico mecânica
- Andamento: cursando
 por Alvadorn » Dom Fev 21, 2010 16:32
por Alvadorn » Dom Fev 21, 2010 16:32
Sua resposta está certíssima, mas meu objetivo era resolver através de senos e cossenos, mas graças ao seu raciocínio eu consegui chegar a resposta através dos senos. Muito obrigado novamente!
-
Alvadorn
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sáb Fev 20, 2010 12:47
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldade
por Alison Bissoli » Qui Dez 03, 2009 13:40
- 6 Respostas
- 3804 Exibições
- Última mensagem por Elcioschin

Dom Dez 06, 2009 13:54
Estatística
-
- Dificuldade
por Mauricio pelinson » Qui Fev 02, 2012 19:22
- 0 Respostas
- 4346 Exibições
- Última mensagem por Mauricio pelinson

Qui Fev 02, 2012 19:22
Sequências
-
- Dificuldade
 por Jhennyfer » Ter Jun 18, 2013 17:04
por Jhennyfer » Ter Jun 18, 2013 17:04
- 5 Respostas
- 5732 Exibições
- Última mensagem por jeniffer05

Dom Mai 11, 2014 15:32
Teoria dos Números
-
- dificuldade em geometria
por joanastefani10 » Seg Set 27, 2010 11:42
- 2 Respostas
- 2401 Exibições
- Última mensagem por JoaoGabriel

Seg Set 27, 2010 14:59
Geometria Plana
-
- Dificuldade na questão
por igorcalfe » Qua Nov 03, 2010 17:56
- 4 Respostas
- 3674 Exibições
- Última mensagem por igorcalfe

Sex Nov 05, 2010 18:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 .
.



