 por Rodrigo Tomaz » Sáb Fev 20, 2010 14:24
por Rodrigo Tomaz » Sáb Fev 20, 2010 14:24
Bom dia!
Estava dando uma olhadinha em sua questão e espero poder ajudá-lo.
No enunciado fornece apenas os ângulos e um lado.
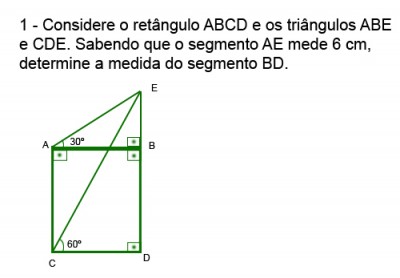
Se você observar o angulo do vértice A é dividido em dois, um de 30° outro de 90°, formando um angulo de 120°.
O angulo do vértice C, também dividido em dois, mede ao todo 90°. Para saber quanto mede a parte restante subtrai-se com os 60º dados obtendo-se 30°.
Se formos olhar como resultou, teremos um triângulo ACE, com ângulos 120°,30 e 30°.
Como o triâgulo observado acima tem dois ângulos iguais, obrigatoriamente terá dois lados iguais (é um triângulo isósceles).
O lado fornecido AE, que mede 6cm, pertence ao triângulo e por não ser oposto ao ângulo diferente o lado AC terá o mesmo valor de 6cm.
Como o lado desejado pertence ao retângulo ABCD, e no mesmo AB=CD e AC=BD logo AC=BD=6cm
Essa questão também pode ser resolvida por outras linhas de raciocínio. Outra por exemplo seria fazer o jogo de senos, cossenos e tangentes descobrindo lado por lado até então chegar no valor desejado.
Eu acho que é isso,
Espero ter te ajudado
- Anexos
-




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)