lsergio_santos,
Boa tarde.
Para que as retas de equações y=mx-8 e y-x/m=0 sejam concorrentes deverá existir um ponto (x,y) iguais para as duas equações, ou seja:
Foi dado que:

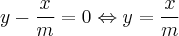
Assim, igualando as duas equações, tem-se:
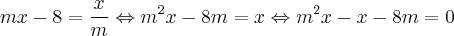
Isolando o x, teremos:
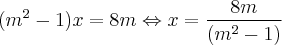
Usando quaisquer uma das equações dadas, podemos determinar o valor de y (usarei a primeira por ser mais simples):

Não sei se estão faltando dados no seu enunciado. Se for só isso mesmo, então quaisquer valores para m, com exceção de:


![m \neq \pm \sqrt[]{1} m \neq \pm \sqrt[]{1}](/latexrender/pictures/44fd1946f9828efa5bf57f4f0ee1532b.png)
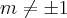
Ou seja, para valores de m onde o denominador se torna zero (m = 1 ou m = -1, conforme calculamos acima), encontraremos consequentemente os valores de x e y, onde as duas retas se coincidem.
Exemplo:
Tomemos m = 5 (pode ser qualquer valor diferente de 1 e -1):
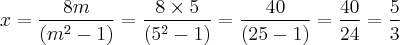
e
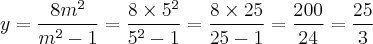
Ou seja:
Para m = 5, o ponto (5/3, 25/3) será o ponto onde as duas retas irão se encontrar e as equações das retas serão:
y = 5x - 8 e y - x/5 = 0, para este caso em particular.
Espero ter auxiliado.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



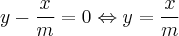
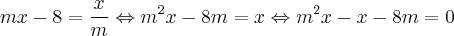
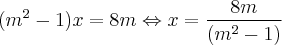



![m \neq \pm \sqrt[]{1} m \neq \pm \sqrt[]{1}](/latexrender/pictures/44fd1946f9828efa5bf57f4f0ee1532b.png)
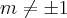
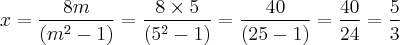
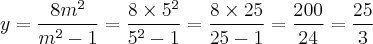

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)