 por Rosi7 » Sáb Mai 23, 2015 09:44
por Rosi7 » Sáb Mai 23, 2015 09:44
Para

e para
![b={2}^{4}.{6}^{3}.{9}^{2} resolva \sqrt[7]{a.b} b={2}^{4}.{6}^{3}.{9}^{2} resolva \sqrt[7]{a.b}](/latexrender/pictures/1106fd7e30fc7e223bcb72dd77237729.png)
-
Rosi7
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Mai 02, 2015 18:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por nakagumahissao » Dom Mai 24, 2015 01:54
por nakagumahissao » Dom Mai 24, 2015 01:54
Rosi7, pelas regras deste fórum você deveria ter detalhado o que já tentou fazer. Desta vez vou responder a questão mas por favor na próxima vez, tente nos dizer o que já foi feito por você para sanarmos sua dúvida e para que não fiquemos aqui apenas resolvendo os seus problemas de modo que você fique sem sem o principal, aprender.
Resolução:
Substituindo-se a e b debaixo da raiz usando os valores dados, teremos:
[1]
![\sqrt[7]{ab} = \sqrt[7]{{3}^{-1} \cdot {81}^{2} \cdot {2}^{4} \cdot {6}^{3} \cdot {9}^{2}} = \sqrt[7]{ab} = \sqrt[7]{{3}^{-1} \cdot {81}^{2} \cdot {2}^{4} \cdot {6}^{3} \cdot {9}^{2}} =](/latexrender/pictures/ab0db810c84ed85e745467922c4d716c.png)
Decompondo-se 81, 6 e 9 tem-se que:
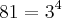
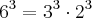
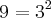
Continuando a resolver [1] e utilizando as várias propriedades da radiciação, temos:
![= \sqrt[7]{{3}^{-1} \cdot {({3}^{4})}^{2} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {({3}^{2})}^{2}} = \sqrt[7]{{3}^{-1} \cdot {3}^{8} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {3}^{4}} = = \sqrt[7]{{3}^{-1} \cdot {({3}^{4})}^{2} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {({3}^{2})}^{2}} = \sqrt[7]{{3}^{-1} \cdot {3}^{8} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {3}^{4}} =](/latexrender/pictures/9f8869fd4bcc173676172b037ee17147.png)
![= \sqrt[7]{{3}^{14} \cdot {2}^{7}} = \sqrt[7]{{3}^{14}} \cdot \sqrt[7]{{2}^{7}} = {3}^{2} \cdot 2 = 9 \times 2 = 18 = \sqrt[7]{{3}^{14} \cdot {2}^{7}} = \sqrt[7]{{3}^{14}} \cdot \sqrt[7]{{2}^{7}} = {3}^{2} \cdot 2 = 9 \times 2 = 18](/latexrender/pictures/8dfae70918eccdb575e4a307c7fa7573.png)
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Rosi7 » Qui Mai 28, 2015 19:02
por Rosi7 » Qui Mai 28, 2015 19:02
Grata e desculpa, esqueci de dizer, mas da próxima vez digo. Esta questão, não é do meu curso, é de um livro de matemática, aí fui fazer, e deu um numero enorme dentro da raiz, pois eu resolvia as potencias, multiplicava e depois ia tirar da raiz.
-
Rosi7
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Mai 02, 2015 18:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por Rosi7 » Qui Mai 28, 2015 19:33
por Rosi7 » Qui Mai 28, 2015 19:33
Os: Achei interessante o poeta, educador Taylor Maly.
Agora a frase: "Eu faço crianças ficarem sentadas por mais de 40 minutos em sala de aula em silêncio absoluto."
Ele deve ser muito bom mesmo. Desculpa, debater o poema com você, mas isso me pareceu um pouco Freiriano.
Embora concorde que:
[...] Eu faço os alunos imaginarem.
Questionarem.
Criticarem.
Eu faço os alunos demonstrarem todos os cálculos matemáticos realizados para chegar às respostas dos problemas.
E faço com que apresentem a redação final como se nunca tivessem produzido um rascunho sequer.
Eu os faço entender que, se você tem um talento, deve segui-lo. [...]
Isso é Vygotsky etc .. e eu amo!
Acho que vou pesquisar sobre Maly.. e continuem colocando as frases, são maravilhosas!
Abraço!
-
Rosi7
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Sáb Mai 02, 2015 18:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relação raiz/polinômio
por engel » Sáb Ago 07, 2010 11:31
- 3 Respostas
- 3331 Exibições
- Última mensagem por Molina

Sáb Ago 07, 2010 16:53
Polinômios
-
- [Polinômio] com raiz complexa
por carolsiva » Qui Jan 09, 2014 09:45
- 3 Respostas
- 3769 Exibições
- Última mensagem por anderson_wallace

Qui Jan 09, 2014 23:24
Polinômios
-
- Integral com Raiz de polinômio no denominador
por sandermec » Qui Jul 24, 2014 02:42
- 0 Respostas
- 2734 Exibições
- Última mensagem por sandermec

Qui Jul 24, 2014 02:42
Cálculo: Limites, Derivadas e Integrais
-
- [raiz da equação] qual a raiz da equação
por lais1906 » Qui Out 11, 2012 14:47
- 3 Respostas
- 2014 Exibições
- Última mensagem por lais1906

Sáb Out 13, 2012 00:17
Equações
-
- Equação Logarítmica - Polinômio
por Rafael16 » Qua Ago 08, 2012 13:19
- 2 Respostas
- 1390 Exibições
- Última mensagem por e8group

Qua Ago 08, 2012 15:43
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e para
e para ![b={2}^{4}.{6}^{3}.{9}^{2} resolva \sqrt[7]{a.b} b={2}^{4}.{6}^{3}.{9}^{2} resolva \sqrt[7]{a.b}](/latexrender/pictures/1106fd7e30fc7e223bcb72dd77237729.png)

 e para
e para ![b={2}^{4}.{6}^{3}.{9}^{2} resolva \sqrt[7]{a.b} b={2}^{4}.{6}^{3}.{9}^{2} resolva \sqrt[7]{a.b}](/latexrender/pictures/1106fd7e30fc7e223bcb72dd77237729.png)

![\sqrt[7]{ab} = \sqrt[7]{{3}^{-1} \cdot {81}^{2} \cdot {2}^{4} \cdot {6}^{3} \cdot {9}^{2}} = \sqrt[7]{ab} = \sqrt[7]{{3}^{-1} \cdot {81}^{2} \cdot {2}^{4} \cdot {6}^{3} \cdot {9}^{2}} =](/latexrender/pictures/ab0db810c84ed85e745467922c4d716c.png)
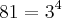
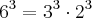
![= \sqrt[7]{{3}^{-1} \cdot {({3}^{4})}^{2} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {({3}^{2})}^{2}} = \sqrt[7]{{3}^{-1} \cdot {3}^{8} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {3}^{4}} = = \sqrt[7]{{3}^{-1} \cdot {({3}^{4})}^{2} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {({3}^{2})}^{2}} = \sqrt[7]{{3}^{-1} \cdot {3}^{8} \cdot {2}^{4} \cdot {3}^{3} \cdot {2}^{3} \cdot {3}^{4}} =](/latexrender/pictures/9f8869fd4bcc173676172b037ee17147.png)
![= \sqrt[7]{{3}^{14} \cdot {2}^{7}} = \sqrt[7]{{3}^{14}} \cdot \sqrt[7]{{2}^{7}} = {3}^{2} \cdot 2 = 9 \times 2 = 18 = \sqrt[7]{{3}^{14} \cdot {2}^{7}} = \sqrt[7]{{3}^{14}} \cdot \sqrt[7]{{2}^{7}} = {3}^{2} \cdot 2 = 9 \times 2 = 18](/latexrender/pictures/8dfae70918eccdb575e4a307c7fa7573.png)


