Dúvida Eq. Diferenciais 2ª Ordem - Ex. Aplicado

[daniel2678]

Gente, estou com problemas para resolver estes exercícios e eles valem nota pra amanhã. Já postei em outros lugares e ninguém conseguiu me fazer entender.


Encontre a carga estacionária e a corrente estacionária em um circuito em
série RCL quando L = 1h, R = 2?, C = 0,25f e E(t) = 50cos(t)V.


e


Ache a carga no capacitor em um circuito em série LRC em t = 0,01s quando
L = 0,05h, R = 2?, C = 0,01f, E(t) = 0V, qo = 5C e i(0) = 0A. Determine a
primeira vez em que a carga sobre o capacitor é igual a zero.


Utilizei a fórmula LQ''+RQ'+Q/C=E(t) no primeiro exercício para chegar em Q"+2Q'+4Q=50cos(t), mas não sei resolver.

O segundo exercício eu só sei a resposta final. Eu estou tentando desde o sábado e nada... É questão de vida ou morte agora... Obrigado!

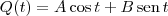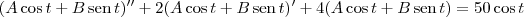
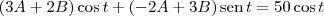
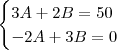
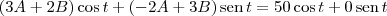
[LuizAquino]

Para resolver a equação diferencial Q"+2Q'+4Q=50cos(t), você precisa usar a estratégia de que a função Q(t) tem o formato:
.

O seu objetivo será determinar as constantes A e B. Para isso, comece substituindo a função na equação diferencial:


Resolvendo as derivadas e arrumando a equação, você obtém:


Agora, basta você resolver o sistema:


Observação
Para armar o sistema basta notar que temos a equação:

[0146251]

Ache a carga no capacitor em um circuito em série LRC em t = 0,01s quando
L = 0,05h, R = 2?, C = 0,01f, E(t) = 0V, qo = 5C e i(0) = 0A. Determine a
primeira vez em que a carga sobre o capacitor é igual a zero.

Conforme a equação acima e faço pela equações lineares com coeficientes contantes.

Então tenho a equação:

0,05d²/dt² + 2 dq/dt + 1/0,01q = 0

então obtenho o resultado e para descobrir c1 e c2 faço q(0)=5 e q'(0)=0

Obtendo então c1 e c2, altero apenas o t pelo 0,01s.

Está correto esse raciocínio ?