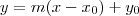por ajurycaba » Ter Abr 28, 2015 14:15
por ajurycaba » Ter Abr 28, 2015 14:15
Encontre a equação da tangente de
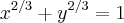
no ponto x =
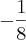
Provavelmente estou fazendo algo errado pois não esta batendo com a resposta do wolfram..
segue minha resolução:
![{x}^{2/3}+{y}^{2/3}=1
\sqrt[3]{{x}^{2}}+\sqrt[3]{{y}^{2}}=1
\sqrt[3]{{y}^{2}}=1-\sqrt[3]{{x}^{2}}
{y}^{2}={(1-\frac{1}{4})}^{3}
y=\sqrt[2]{\frac{27}{64}}
y=±\frac{3\sqrt[2]{3}}{8} \leftarrow encontrei\:meu\:y {x}^{2/3}+{y}^{2/3}=1
\sqrt[3]{{x}^{2}}+\sqrt[3]{{y}^{2}}=1
\sqrt[3]{{y}^{2}}=1-\sqrt[3]{{x}^{2}}
{y}^{2}={(1-\frac{1}{4})}^{3}
y=\sqrt[2]{\frac{27}{64}}
y=±\frac{3\sqrt[2]{3}}{8} \leftarrow encontrei\:meu\:y](/latexrender/pictures/061bcfc1fff280e733d291704c0fc8a3.png)
Agora vamos encontrar os M´s para as equações da tangente:
![{x}^{2/3}+{y}^{2/3}=1
\left( \frac{2}{3{x}^{(1/3)}} \right) + \left( \frac{2}{3{y}^{(1/3)}} \right).y´
\left( \frac{2}{3{y}^{(1/3)}} \right).y´=-\left( \frac{2}{3{x}^{(1/3)}} \right)
y´=\frac{\left({y}^{\left(\frac{1}{3} \right)} \right)}{\left({x}^{\left(\frac{1}{3} \right)} \right)}
{m}_{\left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = \sqrt[2]{3}
{m}_{\left(-\frac{1}{8}, -\frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = -\sqrt[2]{3} {x}^{2/3}+{y}^{2/3}=1
\left( \frac{2}{3{x}^{(1/3)}} \right) + \left( \frac{2}{3{y}^{(1/3)}} \right).y´
\left( \frac{2}{3{y}^{(1/3)}} \right).y´=-\left( \frac{2}{3{x}^{(1/3)}} \right)
y´=\frac{\left({y}^{\left(\frac{1}{3} \right)} \right)}{\left({x}^{\left(\frac{1}{3} \right)} \right)}
{m}_{\left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = \sqrt[2]{3}
{m}_{\left(-\frac{1}{8}, -\frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = -\sqrt[2]{3}](/latexrender/pictures/5e6bbfe3bf76e63ab4651095350e33fe.png)
Eq. da Tg. do ponto
![\left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right) \left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right)](/latexrender/pictures/d069088696a1259bff2e45639b7249d7.png)
:
![y=m.\left( x-{x}_{0} \right)-{y}_{0}
y=\sqrt[2]{3}.\left(x+\frac{1}{8} \right)-\frac{3\sqrt[2]{3}}{8} \right) \rightarrow x\sqrt[2]{3}+\frac{\sqrt[2]{3}}{8} - \frac{3\sqrt[2]{3}}{8} \rightarrow y=x\sqrt[2]{3}+\sqrt[2]{3}.\left(-\frac{1}{3} \right) \rightarrow y=x\sqrt[2]{3}-\frac{\sqrt[2]{3}}{4} y=m.\left( x-{x}_{0} \right)-{y}_{0}
y=\sqrt[2]{3}.\left(x+\frac{1}{8} \right)-\frac{3\sqrt[2]{3}}{8} \right) \rightarrow x\sqrt[2]{3}+\frac{\sqrt[2]{3}}{8} - \frac{3\sqrt[2]{3}}{8} \rightarrow y=x\sqrt[2]{3}+\sqrt[2]{3}.\left(-\frac{1}{3} \right) \rightarrow y=x\sqrt[2]{3}-\frac{\sqrt[2]{3}}{4}](/latexrender/pictures/2f211b38aa3ff69ffc8dee834ca3f713.png)
segue a resposta do wolfram:
https://www.wolframalpha.com/input/?i=t ... x%3D-1%2F8desde já agradeco!
-
ajurycaba
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mar 25, 2015 22:54
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Ter Abr 28, 2015 22:36
por young_jedi » Ter Abr 28, 2015 22:36
a equação da reta é na verdade
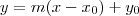
só um pequeno erro de sinal mas sua resolução esta correta
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- TANGENTE
por MERLAYNE » Ter Abr 03, 2012 10:06
- 1 Respostas
- 1283 Exibições
- Última mensagem por MarceloFantini

Ter Abr 03, 2012 14:51
Trigonometria
-
- TANGENTE
por MERLAYNE » Ter Abr 03, 2012 10:14
- 1 Respostas
- 1137 Exibições
- Última mensagem por MarceloFantini

Ter Abr 03, 2012 14:50
Trigonometria
-
- Tangente
por DanielFerreira » Dom Abr 29, 2012 21:15
- 1 Respostas
- 1054 Exibições
- Última mensagem por Russman

Dom Abr 29, 2012 21:58
Trigonometria
-
- Tangente Inversa
por xducke » Qua Jul 22, 2009 02:34
- 1 Respostas
- 3250 Exibições
- Última mensagem por xducke

Qua Jul 22, 2009 18:19
Trigonometria
-
- Função com Tangente
por rafacosme » Qua Jun 16, 2010 15:25
- 2 Respostas
- 1779 Exibições
- Última mensagem por rafacosme

Qua Jun 16, 2010 15:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
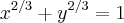 no ponto x =
no ponto x = 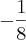
![{x}^{2/3}+{y}^{2/3}=1
\sqrt[3]{{x}^{2}}+\sqrt[3]{{y}^{2}}=1
\sqrt[3]{{y}^{2}}=1-\sqrt[3]{{x}^{2}}
{y}^{2}={(1-\frac{1}{4})}^{3}
y=\sqrt[2]{\frac{27}{64}}
y=±\frac{3\sqrt[2]{3}}{8} \leftarrow encontrei\:meu\:y {x}^{2/3}+{y}^{2/3}=1
\sqrt[3]{{x}^{2}}+\sqrt[3]{{y}^{2}}=1
\sqrt[3]{{y}^{2}}=1-\sqrt[3]{{x}^{2}}
{y}^{2}={(1-\frac{1}{4})}^{3}
y=\sqrt[2]{\frac{27}{64}}
y=±\frac{3\sqrt[2]{3}}{8} \leftarrow encontrei\:meu\:y](/latexrender/pictures/061bcfc1fff280e733d291704c0fc8a3.png)
![{x}^{2/3}+{y}^{2/3}=1
\left( \frac{2}{3{x}^{(1/3)}} \right) + \left( \frac{2}{3{y}^{(1/3)}} \right).y´
\left( \frac{2}{3{y}^{(1/3)}} \right).y´=-\left( \frac{2}{3{x}^{(1/3)}} \right)
y´=\frac{\left({y}^{\left(\frac{1}{3} \right)} \right)}{\left({x}^{\left(\frac{1}{3} \right)} \right)}
{m}_{\left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = \sqrt[2]{3}
{m}_{\left(-\frac{1}{8}, -\frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = -\sqrt[2]{3} {x}^{2/3}+{y}^{2/3}=1
\left( \frac{2}{3{x}^{(1/3)}} \right) + \left( \frac{2}{3{y}^{(1/3)}} \right).y´
\left( \frac{2}{3{y}^{(1/3)}} \right).y´=-\left( \frac{2}{3{x}^{(1/3)}} \right)
y´=\frac{\left({y}^{\left(\frac{1}{3} \right)} \right)}{\left({x}^{\left(\frac{1}{3} \right)} \right)}
{m}_{\left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = \sqrt[2]{3}
{m}_{\left(-\frac{1}{8}, -\frac{3\sqrt[2]{3}}{8} \right)}=-\sqrt[3]{\frac{\frac{3\sqrt[2]{3}}{8}}{-\frac{1}{8}}} \rightarrow -\sqrt[3]{-3\sqrt[2]{3}} = -\sqrt[2]{3}](/latexrender/pictures/5e6bbfe3bf76e63ab4651095350e33fe.png)
![\left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right) \left(-\frac{1}{8}, \frac{3\sqrt[2]{3}}{8} \right)](/latexrender/pictures/d069088696a1259bff2e45639b7249d7.png) :
:![y=m.\left( x-{x}_{0} \right)-{y}_{0}
y=\sqrt[2]{3}.\left(x+\frac{1}{8} \right)-\frac{3\sqrt[2]{3}}{8} \right) \rightarrow x\sqrt[2]{3}+\frac{\sqrt[2]{3}}{8} - \frac{3\sqrt[2]{3}}{8} \rightarrow y=x\sqrt[2]{3}+\sqrt[2]{3}.\left(-\frac{1}{3} \right) \rightarrow y=x\sqrt[2]{3}-\frac{\sqrt[2]{3}}{4} y=m.\left( x-{x}_{0} \right)-{y}_{0}
y=\sqrt[2]{3}.\left(x+\frac{1}{8} \right)-\frac{3\sqrt[2]{3}}{8} \right) \rightarrow x\sqrt[2]{3}+\frac{\sqrt[2]{3}}{8} - \frac{3\sqrt[2]{3}}{8} \rightarrow y=x\sqrt[2]{3}+\sqrt[2]{3}.\left(-\frac{1}{3} \right) \rightarrow y=x\sqrt[2]{3}-\frac{\sqrt[2]{3}}{4}](/latexrender/pictures/2f211b38aa3ff69ffc8dee834ca3f713.png)