 por Adrielly » Qui Fev 11, 2010 11:26
por Adrielly » Qui Fev 11, 2010 11:26
Bom, estou estudando para o vestibular! E me deparei com a seuite questão quanto é
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png)
não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é

como isso??
-
Adrielly
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 11, 2010 11:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Fev 11, 2010 12:10
por Molina » Qui Fev 11, 2010 12:10
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adrielly » Qui Fev 11, 2010 13:41
por Adrielly » Qui Fev 11, 2010 13:41
eu consegui entender até a parte de fatorar o 10, mas e o 2 elevado a 30? como que ele se transformou nesse 1+2² ?
-
Adrielly
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 11, 2010 11:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Fev 11, 2010 14:00
por Molina » Qui Fev 11, 2010 14:00
Ok, vamos lá:
Fazendo a distributiva em
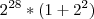
no encontramos

, pois
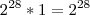
e

Então o que eu fiz foi a operação contrária da distributiva, ou seja, fatorei os termos e coloquei o

em evidência.
Então eu tenho que
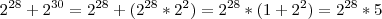
O

continua ali, so que ele está numa forma fatorada. É a mesma coisa que eu escrever
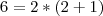
. Caso não tenha ficado claro, informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rojantsch » Sex Fev 19, 2010 12:56
por rojantsch » Sex Fev 19, 2010 12:56
como se resolve potencias que envolvam frações? so to querendo uma ajuda por favor?
eu preciso fazer um exercicio.
-
rojantsch
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Fev 19, 2010 12:49
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Entender o resultado de uma análise de coorelação
por Roniberto » Qua Mai 13, 2009 16:30
- 0 Respostas
- 946 Exibições
- Última mensagem por Roniberto

Qua Mai 13, 2009 16:30
Estatística
-
- Preciso de ajuda com esse exercício
por Dankaerte » Qui Set 10, 2009 19:10
- 2 Respostas
- 6290 Exibições
- Última mensagem por Elcioschin

Ter Abr 13, 2010 14:01
Matrizes e Determinantes
-
- [Integrais] Preciso de ajuda com esse cálculo...
por phvicari » Sáb Set 03, 2011 04:40
- 3 Respostas
- 1860 Exibições
- Última mensagem por LuizAquino

Dom Set 04, 2011 13:30
Cálculo: Limites, Derivadas e Integrais
-
- Preciso saber a fórmula para resolver esse exercício
por Dankaerte » Qui Ago 27, 2009 14:19
- 1 Respostas
- 6967 Exibições
- Última mensagem por Molina

Qui Ago 27, 2009 14:58
Geometria Plana
-
- Como aprender e entender matemática
por Bielto » Sáb Jul 14, 2012 13:55
- 8 Respostas
- 5703 Exibições
- Última mensagem por LuizAquino

Dom Jul 15, 2012 13:18
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png) não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é
não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é  como isso??
como isso??
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png) não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é
não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é  como isso??
como isso??
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png)
![\sqrt[3]{\frac{{2}^{28}(1+{2}^{2})}{2*5}} \sqrt[3]{\frac{{2}^{28}(1+{2}^{2})}{2*5}}](/latexrender/pictures/c83447ebace86cc855540102cbc53ed7.png)
![\sqrt[3]{\frac{{2}^{28}*5}{2*5}} \sqrt[3]{\frac{{2}^{28}*5}{2*5}}](/latexrender/pictures/2c926a1b36a9536d64f26372fba82eeb.png)
![\sqrt[3]{{2^{27}}} \sqrt[3]{{2^{27}}}](/latexrender/pictures/1091c23a1b9db3cddfb26957cefc8126.png)
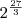




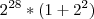 no encontramos
no encontramos  , pois
, pois 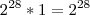 e
e 
 em evidência.
em evidência.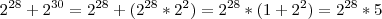
 continua ali, so que ele está numa forma fatorada. É a mesma coisa que eu escrever
continua ali, so que ele está numa forma fatorada. É a mesma coisa que eu escrever 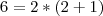 . Caso não tenha ficado claro, informe!
. Caso não tenha ficado claro, informe!




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.