 por yonara » Ter Jan 19, 2010 16:13
por yonara » Ter Jan 19, 2010 16:13
Olá. O meu problema é o seguinte:
A probabilidade de que você resolva corretamente a 1ª questão de uma prova é 1/3 e de que seu colega resolva corretamente é 2/5, sendo que ambos tentam, sozinhos, resolvê-la. Considere o experimento em que se verifica se a questão foi resolvida corretamente ou não pelos dois.
c) qual a probabilidade de pelo menos um resolver a questão corretamente?
Resp: 0,6
___________________________________________________________________
Eu tentei somando as probabilidades de "eu OU o colega" resolver a questão. E depois de "eu E o colega" resolver a questão, já que pede para pelo menos um resolver a questão. E no final multipliquei a probabilidade desses dois eventos, mas não consegui achar o resultado...
-
yonara
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Jun 30, 2009 18:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: medicina veterinária
- Andamento: cursando
 por MarceloFantini » Qua Jan 20, 2010 11:28
por MarceloFantini » Qua Jan 20, 2010 11:28
Bom dia Yonara!
Na situação dada, você concorda que apenas existem quatro casos possíveis:
- A
acerte a questão e B
erre;
- A
acerte a questão e B
acerte também;
- A
erre a questão e B
acerte;
- A
erre e B também
erre.
Portanto, você concorda que a probabilidade de que
pelo menos um acerte é a probabilidade de todos os casos menos o que todos erram? Logo:
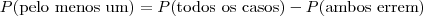




Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por yonara » Qui Jan 21, 2010 00:44
por yonara » Qui Jan 21, 2010 00:44
eu entendi bem! muito obrigada.

-
yonara
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Jun 30, 2009 18:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: medicina veterinária
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Probabilidade simples
por tiagofe » Qua Abr 20, 2011 07:46
- 3 Respostas
- 4540 Exibições
- Última mensagem por tiagofe

Sáb Abr 23, 2011 09:50
Estatística
-
- probabilidade simples
por ezidia51 » Qui Jun 28, 2018 19:54
- 0 Respostas
- 5705 Exibições
- Última mensagem por ezidia51

Qui Jun 28, 2018 19:54
Probabilidade
-
- PROBABILIDADE SIMPLES
por gabrielpacito » Ter Mar 06, 2018 01:52
- 1 Respostas
- 6587 Exibições
- Última mensagem por Gebe

Ter Mar 06, 2018 02:51
Probabilidade
-
- PROBABILIDADE SIMPLES
por gabrielpacito » Ter Mar 06, 2018 01:50
- 1 Respostas
- 5591 Exibições
- Última mensagem por Gebe

Ter Mar 06, 2018 02:30
Probabilidade
-
- PROBABILIDADE SIMPLES
por gabrielpacito » Ter Mar 06, 2018 01:49
- 0 Respostas
- 4160 Exibições
- Última mensagem por gabrielpacito

Ter Mar 06, 2018 01:49
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


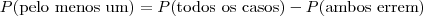









 , avisa que eu resolvo.
, avisa que eu resolvo.

