Questão: No Brasil, os clientes de telefonia móvel podem optar pelos sistemas pré-pago ou pós-pago. Em certa empresa de telefonia móvel, 17 em cada 20 clientes, utilizam o sistema pré-pago. Sendo assim, o número de clientes que utilizam o pré-pago supera o número de clientes do pós-pago em 24,36 milhões. Quantos milhões de clientes são atendidos por essa empresa?
a) 29,58
b)30,25
c)31,20
d) 32,18
e) 34,80
No gabarito a resposta correta é a E. Porém, em meus cálculos esse valor é de 42,98.
Fiz através do cruzamento de informações:
17---------------------------> 24,36
03---------------------------> x
Dessa forma cheguei a:
x= 3.24,36
---------- que dá o resultado 4,2988.
17
Sei que estou fazendo da forma errada e preciso de ajuda.
Grata.
----


 o número total de clientes(medido em milhões), de
o número total de clientes(medido em milhões), de  os que pagam pré-pago(medido em milhões) e
os que pagam pré-pago(medido em milhões) e  os que pagam pós-pago(medido em milhões).
os que pagam pós-pago(medido em milhões).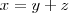 . (1)
. (1)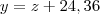 (2)
(2)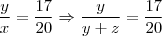 . (3)
. (3)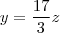 . Daí, unido a informação de (2), temos
. Daí, unido a informação de (2), temos
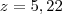 e, portanto,
e, portanto, 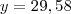 .
. .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

