 por JorgeVidal » Dom Fev 22, 2015 18:00
por JorgeVidal » Dom Fev 22, 2015 18:00
Use a desigualdade de Cauchy-Schwarz para mostrar que:
a) Se

, então
![\frac{1}{2}(\sqrt[2]{a}+\sqrt[2]{b}+\sqrt[2]{c}+\sqrt[2]{d})\geq\sqrt[2]{a+b+c+d} \frac{1}{2}(\sqrt[2]{a}+\sqrt[2]{b}+\sqrt[2]{c}+\sqrt[2]{d})\geq\sqrt[2]{a+b+c+d}](/latexrender/pictures/3a488cde3ffed1afbc446372ab9b2d84.png)
;
b)
![cos\theta.sen\varphi+sin\theta.sin\varphi+cos\varphi\leq\sqrt[]{3} cos\theta.sen\varphi+sin\theta.sin\varphi+cos\varphi\leq\sqrt[]{3}](/latexrender/pictures/7f205316b288935743858e178bf84ac3.png)
, para quaisquer
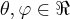
;
c) Se
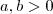
e
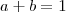
, então

-
JorgeVidal
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Fev 22, 2015 17:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Qua Fev 25, 2015 20:49
por adauto martins » Qua Fev 25, 2015 20:49
a)farei p/ dois num. e extender p/ os quatro...
![{(\sqrt[]{a}-\sqrt[]{b}})^{2}\geq 0\Rightarrow a-2\sqrt[]{a}\sqrt[]{b}+b\succeq 0 {(\sqrt[]{a}-\sqrt[]{b}})^{2}\geq 0\Rightarrow a-2\sqrt[]{a}\sqrt[]{b}+b\succeq 0](/latexrender/pictures/86a4e2b148e79ab349d6649bbc3ed1d1.png)
![\Rightarrow a+b\succeq 2\sqrt[]{a}\sqrt[]{b}\Rightarrow a+2\sqrt[]{a}.\sqrt[]{b}+b\succeq 4\sqrt[]{a}\sqrt[]{b}\Rightarrow {(\sqrt[]{a}+\sqrt[]{b}})^{2}\succeq 4\sqrt[]{a}\sqrt[]{b} \Rightarrow a+b\succeq 2\sqrt[]{a}\sqrt[]{b}\Rightarrow a+2\sqrt[]{a}.\sqrt[]{b}+b\succeq 4\sqrt[]{a}\sqrt[]{b}\Rightarrow {(\sqrt[]{a}+\sqrt[]{b}})^{2}\succeq 4\sqrt[]{a}\sqrt[]{b}](/latexrender/pictures/03aa48a976376a823cdd961341f97555.png)
![\Rightarrow 1/2(\sqrt[]{a}+\sqrt[]{b})\succeq \sqrt[]{a.b}\succeq \sqrt[]{a+b} \Rightarrow 1/2(\sqrt[]{a}+\sqrt[]{b})\succeq \sqrt[]{a.b}\succeq \sqrt[]{a+b}](/latexrender/pictures/70aa8984c260215fc8533e5a2ae01f10.png)
...
b)

![\preceq \left|sen\thet.cos\thetasen\varphi \right|+\left|sen\theta.sen\thetacos\varphi \right|+\left|cos\varphi \right|\preceq (\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2) \preceq \left|sen\thet.cos\thetasen\varphi \right|+\left|sen\theta.sen\thetacos\varphi \right|+\left|cos\varphi \right|\preceq (\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2)](/latexrender/pictures/ae0f8d368ab05c95b0c8561d2dcf4a5e.png)
=
![2/3+(\sqrt[]{3}/2)\prec (\sqrt[]{3}/2).(\sqrt[]{3}/2)=\sqrt[]{3} 2/3+(\sqrt[]{3}/2)\prec (\sqrt[]{3}/2).(\sqrt[]{3}/2)=\sqrt[]{3}](/latexrender/pictures/95fde11370746158fb213481d132c49d.png)
c)sugestao...desiqualdade de bernoulli...
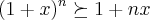
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Teoria dos Números
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números Reais - Simplificar números reais
por ZANGARO » Ter Nov 15, 2011 18:46
- 0 Respostas
- 1945 Exibições
- Última mensagem por ZANGARO

Ter Nov 15, 2011 18:46
Álgebra Elementar
-
- Análise real
por matmatco » Qui Jun 29, 2017 08:28
- 3 Respostas
- 3616 Exibições
- Última mensagem por adauto martins

Qui Jul 13, 2017 13:06
Cálculo: Limites, Derivadas e Integrais
-
- Análise Real/Sequencia
por Raphaelphtp » Seg Jan 16, 2017 15:24
- 1 Respostas
- 2415 Exibições
- Última mensagem por adauto martins

Ter Jan 17, 2017 10:33
Cálculo: Limites, Derivadas e Integrais
-
- Números reais
por citadp » Dom Jun 24, 2012 16:02
- 1 Respostas
- 1761 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
-
- Numeros reais
por vihalmeida » Qui Nov 15, 2012 15:19
- 1 Respostas
- 2200 Exibições
- Última mensagem por DanielFerreira

Qui Nov 15, 2012 18:40
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , então
, então ![\frac{1}{2}(\sqrt[2]{a}+\sqrt[2]{b}+\sqrt[2]{c}+\sqrt[2]{d})\geq\sqrt[2]{a+b+c+d} \frac{1}{2}(\sqrt[2]{a}+\sqrt[2]{b}+\sqrt[2]{c}+\sqrt[2]{d})\geq\sqrt[2]{a+b+c+d}](/latexrender/pictures/3a488cde3ffed1afbc446372ab9b2d84.png) ;
;![cos\theta.sen\varphi+sin\theta.sin\varphi+cos\varphi\leq\sqrt[]{3} cos\theta.sen\varphi+sin\theta.sin\varphi+cos\varphi\leq\sqrt[]{3}](/latexrender/pictures/7f205316b288935743858e178bf84ac3.png) , para quaisquer
, para quaisquer 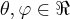 ;
;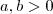 e
e 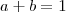 , então
, então 

 , então
, então ![\frac{1}{2}(\sqrt[2]{a}+\sqrt[2]{b}+\sqrt[2]{c}+\sqrt[2]{d})\geq\sqrt[2]{a+b+c+d} \frac{1}{2}(\sqrt[2]{a}+\sqrt[2]{b}+\sqrt[2]{c}+\sqrt[2]{d})\geq\sqrt[2]{a+b+c+d}](/latexrender/pictures/3a488cde3ffed1afbc446372ab9b2d84.png) ;
;![cos\theta.sen\varphi+sin\theta.sin\varphi+cos\varphi\leq\sqrt[]{3} cos\theta.sen\varphi+sin\theta.sin\varphi+cos\varphi\leq\sqrt[]{3}](/latexrender/pictures/7f205316b288935743858e178bf84ac3.png) , para quaisquer
, para quaisquer 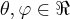 ;
;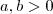 e
e 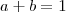 , então
, então 

![{(\sqrt[]{a}-\sqrt[]{b}})^{2}\geq 0\Rightarrow a-2\sqrt[]{a}\sqrt[]{b}+b\succeq 0 {(\sqrt[]{a}-\sqrt[]{b}})^{2}\geq 0\Rightarrow a-2\sqrt[]{a}\sqrt[]{b}+b\succeq 0](/latexrender/pictures/86a4e2b148e79ab349d6649bbc3ed1d1.png)
![\Rightarrow a+b\succeq 2\sqrt[]{a}\sqrt[]{b}\Rightarrow a+2\sqrt[]{a}.\sqrt[]{b}+b\succeq 4\sqrt[]{a}\sqrt[]{b}\Rightarrow {(\sqrt[]{a}+\sqrt[]{b}})^{2}\succeq 4\sqrt[]{a}\sqrt[]{b} \Rightarrow a+b\succeq 2\sqrt[]{a}\sqrt[]{b}\Rightarrow a+2\sqrt[]{a}.\sqrt[]{b}+b\succeq 4\sqrt[]{a}\sqrt[]{b}\Rightarrow {(\sqrt[]{a}+\sqrt[]{b}})^{2}\succeq 4\sqrt[]{a}\sqrt[]{b}](/latexrender/pictures/03aa48a976376a823cdd961341f97555.png)
![\Rightarrow 1/2(\sqrt[]{a}+\sqrt[]{b})\succeq \sqrt[]{a.b}\succeq \sqrt[]{a+b} \Rightarrow 1/2(\sqrt[]{a}+\sqrt[]{b})\succeq \sqrt[]{a.b}\succeq \sqrt[]{a+b}](/latexrender/pictures/70aa8984c260215fc8533e5a2ae01f10.png) ...
...
![\preceq \left|sen\thet.cos\thetasen\varphi \right|+\left|sen\theta.sen\thetacos\varphi \right|+\left|cos\varphi \right|\preceq (\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2) \preceq \left|sen\thet.cos\thetasen\varphi \right|+\left|sen\theta.sen\thetacos\varphi \right|+\left|cos\varphi \right|\preceq (\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2).(\sqrt[]{3}/2)+(\sqrt[]{3}/2)](/latexrender/pictures/ae0f8d368ab05c95b0c8561d2dcf4a5e.png) =
=![2/3+(\sqrt[]{3}/2)\prec (\sqrt[]{3}/2).(\sqrt[]{3}/2)=\sqrt[]{3} 2/3+(\sqrt[]{3}/2)\prec (\sqrt[]{3}/2).(\sqrt[]{3}/2)=\sqrt[]{3}](/latexrender/pictures/95fde11370746158fb213481d132c49d.png)
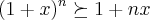 ...
...


 , avisa que eu resolvo.
, avisa que eu resolvo.

