 por matheus_frs1 » Ter Fev 10, 2015 11:33
por matheus_frs1 » Ter Fev 10, 2015 11:33
Dadas as equações
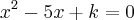
e

, sabe-se que uma das raízes da segunda equação e o dobro de uma das raízes da primeira equação. Sendo

, determine

.
Galera, tentei fazer umas loucuras e cheguei em k = 6, mas fiz inúmeros processos. Alguém me explica uma maneira mais fácil?
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Cleyson007 » Ter Fev 10, 2015 15:29
por Cleyson007 » Ter Fev 10, 2015 15:29
Boa tarde Matheus!
Vamos chamar de "m" e "n" as raízes da primeira equação (x²-5x+k= 0)
Chamaremos de "m" e "2n" as raízes da segunda equação (x² -7x +2k = 0)
Temos que:
m + n = 5
m + 2n= 7
Na primeira equação, temos: m = 5 - n
Substituindo na segunda equação: 5 - n + 2n = 7 ---> n = 2
Como m = 5 - n ---> m = 3
k é o produto das raízes
k= (2)(3) = 6
Comente qualquer dúvida

Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por matheus_frs1 » Qua Fev 11, 2015 00:02
por matheus_frs1 » Qua Fev 11, 2015 00:02
Vlw, Cleyson, vc fez de uma maneira muito mais simples. Eu fiz cada rolo, kkkkkkkkkkkkkk. Muito obrigado
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Cleyson007 » Qua Fev 11, 2015 16:58
por Cleyson007 » Qua Fev 11, 2015 16:58
Olá Matheus, boa tarde!
Foi um prazer ajudar meu amigo

Aproveitando a oportunidade convido-o para que conheça melhor o meu trabalho:
viewtopic.php?f=151&t=13614Qualquer dúvida estou a disposição.
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por matheus_frs1 » Qui Fev 12, 2015 12:16
por matheus_frs1 » Qui Fev 12, 2015 12:16
Parabéns pelo trabalho Cleyson.
Agora uma coisa me chamou atenção... vc disse que atende pelo whatsapp e percebi que o DDD é 38 (região do interior de MG).
Que mal lhe pergunte, de qual cidade vc é? Pergunto isso, pq já morei nessa região, precisamente em Montes Claros.
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Eq Dif] Variação dos Parâmetros
por Bruno G Carneiro » Qua Jun 06, 2012 16:08
- 1 Respostas
- 1100 Exibições
- Última mensagem por nietzsche

Qua Jun 06, 2012 22:03
Cálculo: Limites, Derivadas e Integrais
-
- [Eq Dif] Variação dos Parâmetros
por Bruno G Carneiro » Qua Jun 06, 2012 16:20
- 1 Respostas
- 1244 Exibições
- Última mensagem por Bruno G Carneiro

Qui Jun 07, 2012 19:15
Cálculo: Limites, Derivadas e Integrais
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7734 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13237 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13025 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
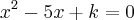 e
e  , sabe-se que uma das raízes da segunda equação e o dobro de uma das raízes da primeira equação. Sendo
, sabe-se que uma das raízes da segunda equação e o dobro de uma das raízes da primeira equação. Sendo  , determine
, determine  .
.
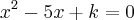 e
e  , sabe-se que uma das raízes da segunda equação e o dobro de uma das raízes da primeira equação. Sendo
, sabe-se que uma das raízes da segunda equação e o dobro de uma das raízes da primeira equação. Sendo  , determine
, determine  .
.





