 por Flavio Casaes » Dom Fev 08, 2015 00:20
por Flavio Casaes » Dom Fev 08, 2015 00:20
Boa noite pessoal, estou começando a estudar integrais e ainda não consegui assimilar um metodo básico e mais simples para optar entre a integração por partes ou substituição. Se alguem puder me ajudar quanto a isso eu agradeço.
Tenho um exemplo resolvido pelo professor que me deixou ainda mais confuso:

No caso dessa integral simples ele resolveu por partes usando: u = x - 1 e dx = dv, até ai beleza...mas o que eu não entendo é porquê eu não posso fazer por substituição usando u = x - 1 e du = dx daí eu teria
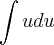
que é mais fácil de resolver.
-
Flavio Casaes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Fev 07, 2015 23:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civíl
- Andamento: cursando
 por nakagumahissao » Dom Fev 08, 2015 21:51
por nakagumahissao » Dom Fev 08, 2015 21:51
Flávio,
Poder usar, você pode, porém seu professor está te passando um exemplo já conhecido, com uma técnica nova para que você perceba que os resultados serão os mesmos. Depois, quando você for resolver exercícios, você vai perceber que é muito mais prático resolver a questão usando esta nova técnica e que as outras aprendidas anteriormente podem até serem usadas e funcionar, mas darão muito mais trabalho, ou ainda, serem impossíveis de serem resolvidas com as técnicas anteriormente aprendidas.
No fim, depois que você aprender todas as técnicas de integração, você simplesmente vai usar aquela que achar mais fácil de se chegar à uma solução.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Flavio Casaes » Dom Fev 08, 2015 23:09
por Flavio Casaes » Dom Fev 08, 2015 23:09
Valeu pela resposta, mas eu perguntei porque eu tentei fazer por substituição mas não deu certo, favor da uma olhada e me sinaliza onde estou errando:
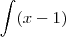
u = x - 1 e du = dx,
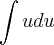
>>>
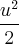
>>>
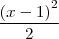
+ C >>>
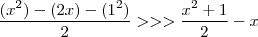
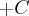
ja na resolução do professor ele fazia por partes:
u=x-1, du=dx, dx=dv, x=v >>> I = (x-1) * x -

>>>

+ C >>>

Tentei simplificar os resultados pra chegar numa resposta em comum, mas minhas limitações matemáticas não permitiram. rs
Se alguém puder me ajudar dizendo onde eu estou errando, se é na operação matemática ou na integral, eu agradeço.
obs: Sei que a dúvida pra alguns pode significar ignorância da minha parte, uma vez que a questão é fácil, mas se entender o início vou poder partir pras mais dificeis e tentar resolver.
grato
-
Flavio Casaes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Fev 07, 2015 23:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civíl
- Andamento: cursando
 por nakagumahissao » Dom Fev 08, 2015 23:36
por nakagumahissao » Dom Fev 08, 2015 23:36
Pode parecer estranho, mas os dois resultados que você encontrou são iguais, ou melhor, semelhantes e ambos, válidos!
Na sua primeira resolução, apesar do resultado correto, havia um erro de sinal em

Que deveria ser positiva.
Seu resultado foi:

Vamos apenas reescrever esse resultado deuma outra forma, lembrando que, o resultado de uma integraçao indefinida nos dá a família de resultados:

Da segunda resolução, você chegou em

Que também podemos reescrever da seguinte maneira :
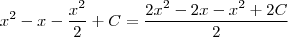

Assim, as duas soluções são válidas e semelhantes
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Flavio Casaes » Seg Fev 09, 2015 09:55
por Flavio Casaes » Seg Fev 09, 2015 09:55
Agradeço muito pela resposta cara, mas não intendi essa ultima simplificação:
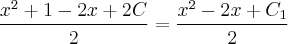
Como o

saiu ?
-
Flavio Casaes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Fev 07, 2015 23:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civíl
- Andamento: cursando
 por nakagumahissao » Seg Fev 09, 2015 09:59
por nakagumahissao » Seg Fev 09, 2015 09:59
MMC. Minimo Múltiplo Comum nas frações
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por nakagumahissao » Seg Fev 09, 2015 10:01
por nakagumahissao » Seg Fev 09, 2015 10:01
2C + 1 = C1
Note que apesar de C1 e C2 serem diferentes, isso não tem grande importância pois o resultado final diz que para toda e qualquer constante, usando a expressão final obtida, teremos toda a família de curvas solução
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por Flavio Casaes » Seg Fev 09, 2015 10:41
por Flavio Casaes » Seg Fev 09, 2015 10:41
Muito obrigado mesmo cara
A questão do m.m.c. eu sabia, mas o que você conseguiu me alertar foi a questão da constante e era isso que tava pegando, pois sempre que tentava simplificar as duas sobrava este valor 1/2 que no caso ai pode ser somado ao C da integral e manter a uniformidade dos resultados. Entendi certo?
De qualquer forma agradeço pela atenção.
-
Flavio Casaes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Fev 07, 2015 23:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civíl
- Andamento: cursando
 por nakagumahissao » Seg Fev 09, 2015 12:32
por nakagumahissao » Seg Fev 09, 2015 12:32
Isso mesmo! Flw. Obrigado por acompanhar
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por Substituição e por Partes
 por Jhenrique » Sáb Set 15, 2012 14:59
por Jhenrique » Sáb Set 15, 2012 14:59
- 23 Respostas
- 31223 Exibições
- Última mensagem por Jhenrique

Qua Set 26, 2012 21:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição e partes
por klueger » Ter Fev 05, 2013 15:42
- 1 Respostas
- 1925 Exibições
- Última mensagem por e8group

Ter Fev 05, 2013 20:34
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] SUBSTITUIÇÃO E POR PARTES
por FERNANDA_03 » Sex Mar 29, 2013 14:00
- 1 Respostas
- 1811 Exibições
- Última mensagem por young_jedi

Sex Mar 29, 2013 16:08
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição ou por partes.
por Sobreira » Sáb Jul 20, 2013 15:03
- 1 Respostas
- 2708 Exibições
- Última mensagem por young_jedi

Sex Jul 26, 2013 20:42
Cálculo: Limites, Derivadas e Integrais
-
- [Integral por partes e substituição]
por vergilxdante » Seg Mar 31, 2014 15:28
- 0 Respostas
- 1831 Exibições
- Última mensagem por vergilxdante

Seg Mar 31, 2014 15:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

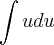 que é mais fácil de resolver.
que é mais fácil de resolver.


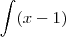
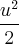 >>>
>>> 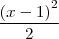 + C >>>
+ C >>> 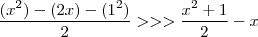
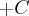
 >>>
>>>  + C >>>
+ C >>> 




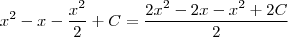

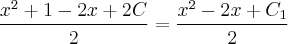
 saiu ?
saiu ?![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.