Tenho um exemplo resolvido pelo professor que me deixou ainda mais confuso:

No caso dessa integral simples ele resolveu por partes usando: u = x - 1 e dx = dv, até ai beleza...mas o que eu não entendo é porquê eu não posso fazer por substituição usando u = x - 1 e du = dx daí eu teria
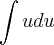 que é mais fácil de resolver.
que é mais fácil de resolver.


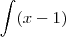
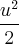 >>>
>>> 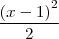 + C >>>
+ C >>> 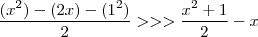
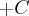
 >>>
>>>  + C >>>
+ C >>> 




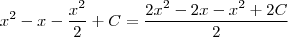

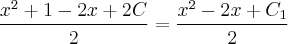
 saiu ?
saiu ?
 .
.



