--> Considere os seguintes números naturais pares 4, 6, 8, ... , 100. Efetuando-se a soma 4! + 6! + 8! + ... + 100!, o algarismo que ocupa a ordem das unidades dessa soma é igual a:
a) 4
b) 2
c) 6
d) 8
Estou tentando assim:
4! = 4 * 3 * 2
6! = 6 * 5 * 4!
8! = 8 * 7 * 6!
10! = 10 * 9 * 8!
Acho que essa relação que apresentei pode ser levada em conta como ponta - pé inicial.. mas não estou conseguindo desenvolver o que o problema pede
Agradeço sua ajuda!
Até mais.
. Percebi que, de 
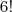pra frente, todos os números terminam em 0. Logo, somando todos, o algarismo da unidade continua sendo o 4.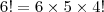
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)