por danielcp » Sex Dez 26, 2014 17:46
por Russman » Sex Dez 26, 2014 23:19
radianos que configura uma volta completa. Ou seja, escolha um ponto qualquer sobre uma circunferência. Desloque este ponto sobre esta circunferência até retornar ao ponto original( isto sempre é possível). Desta forma, você terá compreendido o ângulo de radianos. Porém, nada impede que você continue deslocando este ponto. A partir dos radianos você começa a contar até voltar novamente ao ponto original. Nesse caso terá andando duas voltas completas que configuram 
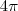radianos. Portanto, dizemos que e são arcos côngruos pois representam, a menos de um número inteiros de "voltas", o mesmo ponto da circunferência: o original.
e 
tais que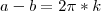 
, onde 
é um inteiro e representa o "número de voltas" efetuadas.
por BELRODES00 » Seg Abr 09, 2012 21:03
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.