 por danielcp » Sex Dez 26, 2014 17:46
por danielcp » Sex Dez 26, 2014 17:46
Olá...
Eu estava estudando trigonometria quando surgiu a determinação geral, que é: para graus ? + 360º*k, k E Z e para radianos ? + 2?*k, k E Z.
Mas eu não consigo entender. Na verdade, eu entendo, porém não sei como aplicar e quero saber se é necessário decorá-la... Alguém poderia me dar um exemplo?
Estamos em período de férias, portanto é impossível ir ao plantão de dúvidas do colégio.
Obrigado.
-
danielcp
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Dez 26, 2014 17:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Sex Dez 26, 2014 23:19
por Russman » Sex Dez 26, 2014 23:19
O, assim chamado, ciclo trigonométrico se divide em

radianos que configura
uma volta completa. Ou seja, escolha um ponto qualquer sobre uma circunferência. Desloque este ponto sobre esta circunferência até retornar ao ponto original( isto sempre é possível). Desta forma, você terá compreendido o ângulo de

radianos. Porém, nada impede que você
continue deslocando este ponto. A partir dos

radianos você começa a contar até voltar novamente ao ponto original. Nesse caso terá andando
duas voltas completas que configuram
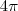
radianos. Portanto, dizemos que

e
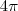
são
arcos côngruos pois representam, a menos de um número inteiros de "voltas", o mesmo ponto da circunferência: o original.
O mesmo procede para dois ângulos quaisquer

e

tais que
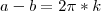
, onde

é um inteiro e representa o "número de voltas" efetuadas.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinação positiva de arcos côngruos
por Maria Livia » Sáb Out 13, 2012 08:30
- 3 Respostas
- 2904 Exibições
- Última mensagem por young_jedi

Sex Out 19, 2012 18:36
Trigonometria
-
- Arcos congruos
por Maria Livia » Sáb Out 13, 2012 08:22
- 1 Respostas
- 3726 Exibições
- Última mensagem por young_jedi

Sáb Out 13, 2012 11:36
Trigonometria
-
- [TRIGONOMETRIA expressão geral dos arcos]
 por BELRODES00 » Seg Abr 09, 2012 21:03
por BELRODES00 » Seg Abr 09, 2012 21:03
- 0 Respostas
- 1475 Exibições
- Última mensagem por BELRODES00

Seg Abr 09, 2012 21:03
Trigonometria
-
- Determinação de divisores
por Abelardo » Seg Mar 07, 2011 00:50
- 4 Respostas
- 3127 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 20:14
Álgebra Elementar
-
- determinação de ponto
por wanderley argenton » Seg Mai 28, 2012 13:58
- 1 Respostas
- 3222 Exibições
- Última mensagem por LuizAquino

Seg Mai 28, 2012 17:42
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 radianos que configura
radianos que configura 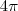 radianos. Portanto, dizemos que
radianos. Portanto, dizemos que  e
e  tais que
tais que 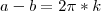 , onde
, onde  é um inteiro e representa o "número de voltas" efetuadas.
é um inteiro e representa o "número de voltas" efetuadas.


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.