 por Renan1434 » Ter Dez 16, 2014 16:00
por Renan1434 » Ter Dez 16, 2014 16:00
Dada a função
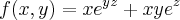
determine:
a) Taxa de variação de f no ponto P=(-2,1,1) na direção do vetor v= (1,-2,3)
b) Taxa máxima de f no ponto P=(-2,1,1) e a direção em que isto ocorre
-
Renan1434
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Dez 15, 2014 23:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por adauto martins » Qua Dez 17, 2014 15:39
por adauto martins » Qua Dez 17, 2014 15:39
a)

![=(({e}^{yz}),(xy{e}^{yz}+x{e}^{z}).(1/\sqrt[]{14},-2/\sqrt[]{14}) =(({e}^{yz}),(xy{e}^{yz}+x{e}^{z}).(1/\sqrt[]{14},-2/\sqrt[]{14})](/latexrender/pictures/d1b67fd322c615dd2cdb901a6b7d3703.png)
![\Rightarrow (\partial f(-2,1)/\partial z)=({e},-4{e}).(1/\sqrt[]{14},-2/\sqrt[]{14})=e/\sqrt[]{14}+8e/\sqrt[]{14}=9e/\sqrt[]{14} \Rightarrow (\partial f(-2,1)/\partial z)=({e},-4{e}).(1/\sqrt[]{14},-2/\sqrt[]{14})=e/\sqrt[]{14}+8e/\sqrt[]{14}=9e/\sqrt[]{14}](/latexrender/pictures/da963b4d00fc361137cdae2a2f7f0592.png)
b)
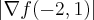
...a direçao da taxa maxima sera a direçao do gradiente...
![(\nabla f(x,y)).{u}_{z}=(\partial f/\partial x,\partial f/\partial y).(-2/\sqrt[]{14},1/\sqrt[]{14}) (\nabla f(x,y)).{u}_{z}=(\partial f/\partial x,\partial f/\partial y).(-2/\sqrt[]{14},1/\sqrt[]{14})](/latexrender/pictures/87f630b9f6efd06e76a47b4a05d34587.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada direcional
por barbara-rabello » Seg Out 15, 2012 20:40
- 9 Respostas
- 5698 Exibições
- Última mensagem por barbara-rabello

Qui Out 18, 2012 12:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivada Direcional
por bruuno » Seg Nov 25, 2013 16:45
- 1 Respostas
- 1798 Exibições
- Última mensagem por Bravim

Ter Nov 26, 2013 03:20
Cálculo: Limites, Derivadas e Integrais
-
- Derivada direcional
 por Jadiel Carlos » Seg Nov 21, 2016 11:14
por Jadiel Carlos » Seg Nov 21, 2016 11:14
- 2 Respostas
- 5874 Exibições
- Última mensagem por Jadiel Carlos

Qui Nov 24, 2016 01:16
Cálculo: Limites, Derivadas e Integrais
-
- [Gradiente e derivada direcional]
por dulifs » Seg Out 31, 2011 15:22
- 2 Respostas
- 4888 Exibições
- Última mensagem por dulifs

Seg Out 31, 2011 18:14
Cálculo: Limites, Derivadas e Integrais
-
- Questão de derivada direcional e gradiente
por Cristiano Tavares » Dom Mai 29, 2011 11:25
- 2 Respostas
- 3805 Exibições
- Última mensagem por Cristiano Tavares

Dom Mai 29, 2011 19:35
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
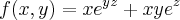 determine:
determine:
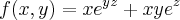 determine:
determine:

![=(({e}^{yz}),(xy{e}^{yz}+x{e}^{z}).(1/\sqrt[]{14},-2/\sqrt[]{14}) =(({e}^{yz}),(xy{e}^{yz}+x{e}^{z}).(1/\sqrt[]{14},-2/\sqrt[]{14})](/latexrender/pictures/d1b67fd322c615dd2cdb901a6b7d3703.png)
![\Rightarrow (\partial f(-2,1)/\partial z)=({e},-4{e}).(1/\sqrt[]{14},-2/\sqrt[]{14})=e/\sqrt[]{14}+8e/\sqrt[]{14}=9e/\sqrt[]{14} \Rightarrow (\partial f(-2,1)/\partial z)=({e},-4{e}).(1/\sqrt[]{14},-2/\sqrt[]{14})=e/\sqrt[]{14}+8e/\sqrt[]{14}=9e/\sqrt[]{14}](/latexrender/pictures/da963b4d00fc361137cdae2a2f7f0592.png)
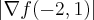 ...a direçao da taxa maxima sera a direçao do gradiente...
...a direçao da taxa maxima sera a direçao do gradiente...![(\nabla f(x,y)).{u}_{z}=(\partial f/\partial x,\partial f/\partial y).(-2/\sqrt[]{14},1/\sqrt[]{14}) (\nabla f(x,y)).{u}_{z}=(\partial f/\partial x,\partial f/\partial y).(-2/\sqrt[]{14},1/\sqrt[]{14})](/latexrender/pictures/87f630b9f6efd06e76a47b4a05d34587.png) ...
...
