 por Ana_Bela » Sáb Dez 13, 2014 22:51
por Ana_Bela » Sáb Dez 13, 2014 22:51
Dado os pontos A(3,m-1,-4) e B(8,2m-1,m), determine m de modo que o módulo do vetor AB seja igual a raiz quadrada de 35.
Obs: Gostaria que alguém visse se está certo da maneira que resolvi ai embaixo, e se tiver algum erro' favor me comunicar e ensinar a fazer o certo.
Minha Resposta :
![\left|AB\right|=\sqrt[2]{35} \left|AB\right|=\sqrt[2]{35}](/latexrender/pictures/c52ad128aa7583a834f286085fe9e804.png)
![\sqrt[2]{{5}^{2}+\left({m-2}\right)^{2}+\left({m+4}\right)^{2}}=\sqrt[2]{35} \sqrt[2]{{5}^{2}+\left({m-2}\right)^{2}+\left({m+4}\right)^{2}}=\sqrt[2]{35}](/latexrender/pictures/4a9a384d83c8e067d4230149688b2fde.png)
desenvolvendo
![\sqrt[2]{{2m}^{2}+4m+45}=\sqrt[2]{35} \sqrt[2]{{2m}^{2}+4m+45}=\sqrt[2]{35}](/latexrender/pictures/c8d66090a202e2786e1e7c5700345b61.png)
desenvolvi a expressão e no final deu' uma equação do 2º grau, onde m = 1 ou m = -3
-
Ana_Bela
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 27, 2014 10:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por Russman » Sáb Dez 13, 2014 23:05
por Russman » Sáb Dez 13, 2014 23:05
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Ana_Bela » Dom Dez 14, 2014 12:26
por Ana_Bela » Dom Dez 14, 2014 12:26
Russman' vlw pela alerta' mas aqui AB é B - A = então é
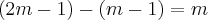
vetor AB = (5,m,m+4)
Terminei aqui é deu m = -1 ou m = -3
Agora espero que esteja certo!
-
Ana_Bela
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 27, 2014 10:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida na aplicação de Modulo no vetor
por PatyMCastro » Qua Abr 20, 2011 14:47
- 6 Respostas
- 3527 Exibições
- Última mensagem por PatyMCastro

Qua Abr 27, 2011 00:34
Geometria Analítica
-
- [geometria analítica e calculo vetorial] modulo de um vetor
por Suellem Albuquerque » Sex Mar 28, 2014 15:36
- 0 Respostas
- 1175 Exibições
- Última mensagem por Suellem Albuquerque

Sex Mar 28, 2014 15:36
Geometria Analítica
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4896 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
-
- [Curvas] Encontrar o vetor posição dado vetor aceleração
 por amigao » Sex Mai 09, 2014 16:37
por amigao » Sex Mai 09, 2014 16:37
- 1 Respostas
- 2083 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 17:25
Geometria Analítica
-
- [Vetor diretor] Encontrando um vetor diretor
por amigao » Sex Mai 17, 2013 13:19
- 2 Respostas
- 8387 Exibições
- Última mensagem por amigao

Sáb Mai 18, 2013 20:12
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left|AB\right|=\sqrt[2]{35} \left|AB\right|=\sqrt[2]{35}](/latexrender/pictures/c52ad128aa7583a834f286085fe9e804.png)
![\sqrt[2]{{5}^{2}+\left({m-2}\right)^{2}+\left({m+4}\right)^{2}}=\sqrt[2]{35} \sqrt[2]{{5}^{2}+\left({m-2}\right)^{2}+\left({m+4}\right)^{2}}=\sqrt[2]{35}](/latexrender/pictures/4a9a384d83c8e067d4230149688b2fde.png) desenvolvendo
desenvolvendo ![\sqrt[2]{{2m}^{2}+4m+45}=\sqrt[2]{35} \sqrt[2]{{2m}^{2}+4m+45}=\sqrt[2]{35}](/latexrender/pictures/c8d66090a202e2786e1e7c5700345b61.png)


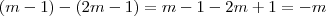

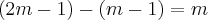

 .
.



