Considere V um espaço vetorial e
 elementos de V. Considere U o subespaço de V gerado por tais n elementos. Dizer que o conjunto {
elementos de V. Considere U o subespaço de V gerado por tais n elementos. Dizer que o conjunto { } é linearmente dependente é o mesmo que dizer que a dimensão do espaço
} é linearmente dependente é o mesmo que dizer que a dimensão do espaço(A) U é igual a n.
(B) U é menor do que n.
(C) U é menor do que a dimensão do espaço V.
(D) V é menor do que a dimensão do espaço U.
(E) V é a dimensão do espaço U adicionada a n.
O gabarito diz LETRA B, mas qual seria o erro na LETRA C?
Grato


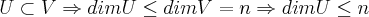


 .
.



