 por Ana_Bela » Qui Nov 27, 2014 11:08
por Ana_Bela » Qui Nov 27, 2014 11:08
Considerando somente o efeito da gravidade e desprezando a resistência do ar, um projétil é arremessado verticalmente do solo, com uma velocidade inicial de 70 m/s. Sabendo que, no caso em questão a altura (s) em metros e o tempo (t) em segundos após o lançamento, é dado por s(t)=
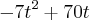
, determine a altura máxima que o projétil atinge:
Obs: eu fiz o yv=

que deu 175 m, esta será a altura máxima?
Gostaria de saber aonde esse 70 m/s da velocidade inicial se encaixa?
-
Ana_Bela
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Nov 27, 2014 10:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por adauto martins » Qui Nov 27, 2014 11:46
por adauto martins » Qui Nov 27, 2014 11:46
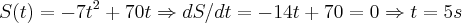
,como
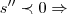
t e o tempo maximo(maior)...logo
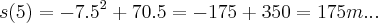
...eq.da velocidade(cinematica)...
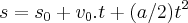
,
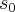
espaço inicial,
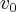
velocidade inicial,e a aceleraçao...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2007 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
-
- Derivada através de Ponto Máximo - Otimização
por Suriano » Qua Mai 06, 2009 20:42
- 3 Respostas
- 6215 Exibições
- Última mensagem por Suriano

Qua Mai 13, 2009 21:39
Cálculo
-
- [calculo] extremos;ponto de minimo e maximo
por beel » Dom Out 30, 2011 19:15
- 2 Respostas
- 2143 Exibições
- Última mensagem por LuizAquino

Seg Out 31, 2011 14:54
Cálculo: Limites, Derivadas e Integrais
-
- [Ponto máximo de uma função]- Pressão sanguínea.
por alicemneves » Seg Mai 28, 2012 00:20
- 7 Respostas
- 5367 Exibições
- Última mensagem por Russman

Qui Mai 31, 2012 22:58
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] extremos;ponto de minimo e maximo
 por citadp » Qua Jun 20, 2012 11:42
por citadp » Qua Jun 20, 2012 11:42
- 1 Respostas
- 1677 Exibições
- Última mensagem por e8group

Qua Jun 20, 2012 13:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
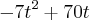 , determine a altura máxima que o projétil atinge:
, determine a altura máxima que o projétil atinge: que deu 175 m, esta será a altura máxima?
que deu 175 m, esta será a altura máxima?
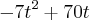 , determine a altura máxima que o projétil atinge:
, determine a altura máxima que o projétil atinge: que deu 175 m, esta será a altura máxima?
que deu 175 m, esta será a altura máxima?
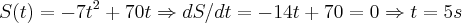 ,como
,como 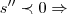 t e o tempo maximo(maior)...logo
t e o tempo maximo(maior)...logo 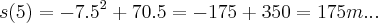 ...eq.da velocidade(cinematica)...
...eq.da velocidade(cinematica)...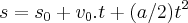 ,
,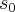 espaço inicial,
espaço inicial,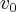 velocidade inicial,e a aceleraçao...
velocidade inicial,e a aceleraçao...


 , avisa que eu resolvo.
, avisa que eu resolvo.

