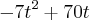 , determine a altura máxima que o projétil atinge:
, determine a altura máxima que o projétil atinge:Obs: eu fiz o yv=
 que deu 175 m, esta será a altura máxima?
que deu 175 m, esta será a altura máxima?Gostaria de saber aonde esse 70 m/s da velocidade inicial se encaixa?

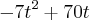 , determine a altura máxima que o projétil atinge:
, determine a altura máxima que o projétil atinge: que deu 175 m, esta será a altura máxima?
que deu 175 m, esta será a altura máxima?
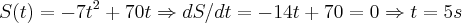 ,como
,como 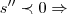 t e o tempo maximo(maior)...logo
t e o tempo maximo(maior)...logo 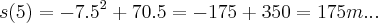 ...eq.da velocidade(cinematica)...
...eq.da velocidade(cinematica)...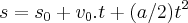 ,
,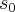 espaço inicial,
espaço inicial,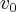 velocidade inicial,e a aceleraçao...
velocidade inicial,e a aceleraçao...
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: