[Exercício de Cálculo - Limites]
Boa tarde, tenho uma professora de cálculo muito ruim, não sabe explicar nada, e dá alguns exercício, muito difíceis de resolver. Fiquei 42 anos sem estudar e voltei agora, estou tendo muita dificuldade na matéria. Preciso de ajuda.
Grato, Jáder
Ola, seguem as questões.
1) Considere o gráfico da figura e responda as questões a seguir:
a) Quais os limites de x tendendo aos valores a, o e b?
b) Existe limite da função quando x tende a menos infinito?
c) Existe limite da função quando x tende a mais infinito?
O que você pode afirmar a respeito dos valores c, d, e, g e h?



 ,sao limites de valores aproximando-se de a,pela direita...ou seja por valores maiores q.a(
,sao limites de valores aproximando-se de a,pela direita...ou seja por valores maiores q.a( )...
)... ,sao limites de valores aproximando-se pela esquerda de a,ou seja ,valores
,sao limites de valores aproximando-se pela esquerda de a,ou seja ,valores  ...quando esses valores sao iguais dizemos q. existe o limite em a,e seu valor sera y=f(a) p/ funçoes continuas...dito isso vamos a resoluçao:
...quando esses valores sao iguais dizemos q. existe o limite em a,e seu valor sera y=f(a) p/ funçoes continuas...dito isso vamos a resoluçao: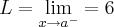 ,acho ser 6 mesmo,e a imagem(eixo yy) da bolinha aberta...
,acho ser 6 mesmo,e a imagem(eixo yy) da bolinha aberta...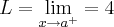 ....
.... ...
...
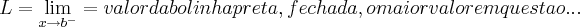
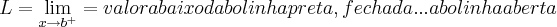 ...escrevo assim pq nao consigo enxergar os valores do grafico...em funçao do exposto acima,resolva as outras questoes...
...escrevo assim pq nao consigo enxergar os valores do grafico...em funçao do exposto acima,resolva as outras questoes...




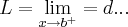
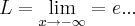
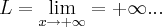
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)