 por neoreload » Qua Nov 19, 2014 23:18
por neoreload » Qua Nov 19, 2014 23:18
Pessoal, como resolve essa:
Calcule a area da região limitada pelas curvas
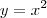
e

.
Eu tentei fazer colocando o
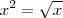
. Sei que é simples, mas meio que esqueci :( . O que faz a partir dai? e no caso eu não tenho a resposta, ai não sei como fazer e nem se estaria chegando no resultado certo. Agradeço quem puder deixar o passo a passo.
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Qui Nov 20, 2014 10:39
por adauto martins » Qui Nov 20, 2014 10:39
primeiramente achar a regiao,no caso

,o ponto onde as curvas se igulam ou seja
![{x}^{2}=\sqrt[]{x} {x}^{2}=\sqrt[]{x}](/latexrender/pictures/2754f1126d721295c7db5f4a47ae5323.png)
...logo teremos
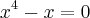
,cujas raizes serao x=0,x=1(raiz de multiplicidade 3)...no intervalo [0,1]
![\sqrt[]{x}\succ {x}^{2}\Rightarrow A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx \sqrt[]{x}\succ {x}^{2}\Rightarrow A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx](/latexrender/pictures/a7616fe17a20b74a09d11516a9486591.png)
...
![A=\int_{0}^{1}({x}^{1/2})dx-\int_{0}^{1}({x}^{2})dx=(2/3){x}^{3/2}-(1/3){x}^{3}[0,1]=(2/3)-(1/3)=1/3 A=\int_{0}^{1}({x}^{1/2})dx-\int_{0}^{1}({x}^{2})dx=(2/3){x}^{3/2}-(1/3){x}^{3}[0,1]=(2/3)-(1/3)=1/3](/latexrender/pictures/0502650a161801cf03ebe167110caca1.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral para calculo de area
por ariclenesmelo » Qua Nov 07, 2012 23:56
- 1 Respostas
- 1636 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 01:05
Cálculo: Limites, Derivadas e Integrais
-
- [Duvida] Uso da integral para area !
por lucasAS » Sáb Mai 31, 2014 19:09
- 1 Respostas
- 1576 Exibições
- Última mensagem por alienante

Dom Jun 01, 2014 10:36
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] area por integral
 por beel » Dom Nov 20, 2011 22:49
por beel » Dom Nov 20, 2011 22:49
- 1 Respostas
- 1382 Exibições
- Última mensagem por LuizAquino

Seg Nov 21, 2011 00:16
Cálculo: Limites, Derivadas e Integrais
-
- Calculo 2 integral de area
por gustavogvm » Ter Set 10, 2013 11:44
- 0 Respostas
- 1429 Exibições
- Última mensagem por gustavogvm

Ter Set 10, 2013 11:44
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de área INTEGRAL
por jccp » Dom Out 06, 2013 15:17
- 1 Respostas
- 2388 Exibições
- Última mensagem por e8group

Dom Out 06, 2013 22:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
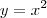 e
e  .
. 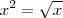 . Sei que é simples, mas meio que esqueci :( . O que faz a partir dai? e no caso eu não tenho a resposta, ai não sei como fazer e nem se estaria chegando no resultado certo. Agradeço quem puder deixar o passo a passo.
. Sei que é simples, mas meio que esqueci :( . O que faz a partir dai? e no caso eu não tenho a resposta, ai não sei como fazer e nem se estaria chegando no resultado certo. Agradeço quem puder deixar o passo a passo.

 ,o ponto onde as curvas se igulam ou seja
,o ponto onde as curvas se igulam ou seja ![{x}^{2}=\sqrt[]{x} {x}^{2}=\sqrt[]{x}](/latexrender/pictures/2754f1126d721295c7db5f4a47ae5323.png) ...logo teremos
...logo teremos 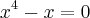 ,cujas raizes serao x=0,x=1(raiz de multiplicidade 3)...no intervalo [0,1]
,cujas raizes serao x=0,x=1(raiz de multiplicidade 3)...no intervalo [0,1]![\sqrt[]{x}\succ {x}^{2}\Rightarrow A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx \sqrt[]{x}\succ {x}^{2}\Rightarrow A=\int_{0}^{1}(\sqrt[]{x}-{x}^{2})dx](/latexrender/pictures/a7616fe17a20b74a09d11516a9486591.png) ...
...![A=\int_{0}^{1}({x}^{1/2})dx-\int_{0}^{1}({x}^{2})dx=(2/3){x}^{3/2}-(1/3){x}^{3}[0,1]=(2/3)-(1/3)=1/3 A=\int_{0}^{1}({x}^{1/2})dx-\int_{0}^{1}({x}^{2})dx=(2/3){x}^{3/2}-(1/3){x}^{3}[0,1]=(2/3)-(1/3)=1/3](/latexrender/pictures/0502650a161801cf03ebe167110caca1.png)
